Как определить удельный объем энтальпию энтропию влажного пара

Как правильно определять основные физико-химические характеристики водяного пара

Расчет степени насыщенности и удельного объёма водяного пара

Задача 37.
Водяной пар при атмосферном давлении имеет температуру t = 126,09 0 С. Определить степень его насыщенности и удельный объем.
Решение:
По таблицам теплофизических свойств водяного пара находим, что температуре t = 126,09 0 С соответствует давление насыщения Р_н = 2,4 . 10 -5 Па. По формуле:
= Р_i/Р_н, где

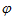
ф — степень насыщенности; Рi — давление водяного пара, 101325 Па; Рн — давление насыщенного пара при заданной температуре.

= (1,01325 . 10-5)/(2,4 . 10-5) = 0,422.

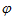
Удельный объем пара рассчитаем по формуле:

Ri – газовая постоянная водяного пара, равная 461,58 Дж/(кг . К); T – температура пара, К.

v_i = (R_i . T)/Р_i = [461,58 . (126,09 + 273)]/(1,01325 . 10-5) = 1,818 м 3 /кг.

Ответ: 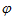= 0,422; v_i = 1,818 м 3 /кг.

Определение удельной энтальпии водяного пара

Задача 38.
Пар при температуре t = 85,95 0 С имеет удельный объем vп = 2,732 м 3 /кг. Определить удельную энтальпию пара.
Решение:
1. Находим плотность пара по формуле:

Р_п = 1/vi = 1/2,732 = 0,366 кг/м 3 .

2. Расчет степени сухости пара

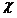
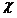
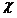
Согласно таблличным данным, температуре t = 85,95 0 С соответствует плотность насыщенного пара рн = 0,366 кг/м 3 . Поскольку рп = рн, то в задаче задан сухой пар. По формуле = Р_п/Р_н ) находим степень сухости пара:

= 0,366/0,366 = 1.

= 1, что соответствует сухому насыщенному пару.

3. Расчет энтальпии пара

Расчет энтальпии пара проводим по формуле:

i_x = i’ * r * 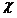, где

i’ — удельная энтальпия кипящей воды; r — удельная теплота парообразования; — степень сухости влажного пара; ix — энтальпия пара.

По таблице приложения для t = 85,95 0С определяем удельную энтальпию кипящей воды и удельную теплоту парообразования i_x = 359,93 кДж/кг, r = 2293,64 кДж/кг.

i_x = 359,93 . 2293,64 . 1 = 825549,8452 кДж/кг.

Ответ: i_x = 825549,8452 кДж/кг.

Относительная упругость, плотность и давление перегретого пара

Задача 39.
Относительная упругость пара при температуре t = 150 0 С составляет ф = 80%. Определить плотность и удельную энтальпию пара.
Решение:
Пар, заданный в задаче, – перегретый. По таблице приложения для температуры t = 150 0 С определяем давление насыщения и плотность насыщенного пара: Р_н = 476000 Па, Р_п = 2,547 кг/м 3 .

1. Расчет плотности заданного пара

Плотности заданного пара находим по формуле:

= Р_i/Р_н, где

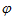
Р_i — плотность заданного пара; рн = плотность насыщенного пара.

Р_i = 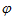. Р_н = 0,8 . 2,547 = 2,0376 кг/м 3 .

2. Расчет давления перегретого пара

Давления перегретого пара рассчитаем по формуле:

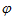
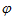
= Р_t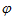/Р_н, где

— относительная упругость пара при заданной температуре; рп =давление насыщенияпара.

Р_t = . Р_п = 0,8 . 476000 = 380800 кг/м 3 .

По таблице приложения находим, что такое давление является насыщенным при температуре t_н = 119,7 2 0 С. Таким образом, пар перегрет от температуры насыщения tн = 119,7 0 С до температуры t = 150 0 С. По таблице определяем удельную теплоемкость пара для этого диапазона температуры, которая оказывается равной сп = 2,114 кДж/(кг . К). По табл. 1 приложения для tн = 119,7 0 С находим удельную энтальпию насыщенного пара i’ = 2704,59 кДж/кг.

3. Расчет удельной энтальпии перегретого пара

По формуле [i_t = i’ . С_п(t -t’)] рассчитываем удельную энтальпию перегретого пара, получим:

i_t = 2704,59 . 2,114(150 -119,7) = 173240,34 кДж/кг.

Ответ: Рi = 2,0376 кг/м 3 ; i_t = 173240,34 кДж/кг.

Источник статьи: http://buzani.ru/zadachi/fizicheskaya-khimiya/1665-svojstva-vodyanogo-para-zadachi-37-39

Energy
education

сайт для тех, кто хочет изучать энергетику

Термодинамика и тепломассообмен

Агрегатное состояние вещества

Агрегатное состояние — состояние вещества, характеризующееся определёнными качественными свойствами — способностью или неспособностью сохранять объём и форму, наличием или отсутствием дальнего и ближнего порядка и другими. Изменение агрегатного состояния сопровождается скачкообразным изменением свободной энергии, энтропии, плотности и других основных физических свойств.

Примеры решения задач по теме «Водяной пар»

1. Определить энтальпию, удельный объем и энтропию и внутреннюю энергию пара, если дано: $p = 0.5$ МПа, $x = 0.9$.

2. Определить энтальпию, удельный объем, энтропию и внутреннюю энергию пара, если дано: $t = 5$ °С, $x = 0.7$.

3. Найти давление, удельный объем и плотность воды, если она находится в состоянии кипения и температура ее равна $200$ °C.

4. На паропроводе насыщенного пара установлен термометр, показывающий $t = 170$ °С. Определить, каково было бы показание манометра на этом паропроводе. Атмосферное давление принять равным $1$ ат.

5. При постоянном давлении $p = 1.0$ МПа смешиваются две порции водяного пара. Масса пара первой порции $M_1 = 200$ кг, его степень сухости $x_1 = 0.85$. Масса пара второй порции $M_2 = 80$ кг, степень сухости $x_2 = 0.10$. Определить степень сухости пара в образовавшейся смеси и его полную энтальпию $Н$ (кДж).

6. В сосуде находится влажный насыщенный пар. Его масса $М = 100$ кг и параметры $t_1= 220$ °C, $x_1= 0.64$. В сосуде отсепарировано и удалено $20$ кг воды, причем давление все время поддерживалось постоянным. Определить параметры $p$, $v$, $h$, $s$ оставшегося в сосуде пара.

7. В барабане котельного агрегата находится кипящая вода и над ней водяной пар под давлением $р = 9$ МПа (давление абсолютное). Масса воды $М = 5000$ кг. Объем барабана $V = 8$ м 3 . Какова масса пара, находящегося над зеркалом испарения, если пар считать сухим насыщенным?

8. Определить параметры $t$, $v$, $h$, $s$ и $u$ влажного насыщенного пара, если его давление (абсолютное) $p = 0.2$ бар, а степень сухости $x = 0.95$.

9. Определить объем резервуара, заполненного влажным паром со степенью сухости $x = 0.9$, если масса пара $M = 160$ кг, а температура в резервуаре $t = 120$ °С.

10. Определить теплоту парообразования $r$ при абсолютном давлении $p = 1$ MПа.

11. По трубопроводу течет водяной пар при давлении $p = 20$ бар и степени сухости $x = 0.96$ со скоростью $W = 10$ м/с. Расход пара $М = 5000$ кг/ч. Определить внутренний диаметр трубы.

12. Определить состояние водяного пара при $p = 15$ бар, если на его получение из воды с температурой $0$ °С было затрачено $2400$ кДж/кг теплоты.

13. В закрытом сосуде объемом $10$ м 3 находится влажный насыщенный водяной пар с абсолютным давлением $p = 1.8$ МПа. В объеме пара содержится $50$ кг жидкости. Определить массу паровой фазы в сосуде и степень сухости пара.

14. Определить расход тепла в пароперегревателе котельного агрегата на $1$ кг пара, если параметры при входе $p = 80$ бар и $x_1 = 0.95$; при выходе $t = 500$ °C.

Администратор сайта: Колосов Михаил
email:
Copyright © 2011-2021. All rights reserved.

Источник статьи: http://www.energyed.ru/Term/TermSolution07

А. И. Бородин Лекции по технической термодинамикЕ

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

5.3. Определение параметров воды и водяного пара

В силу сложности уравнения состояния для водяного пара при расчетах на микрокалькуляторах (в инженерной практике) его заменяют термодинамическими таблицами и диаграммами, составленными на основе теоретических расчетов и экспериментальных данных [10,11]. В этих таблицах приводятся параметры однофазных состояний воды и пара, причем за нулевое состояние, от которого отсчитываются внутренняя энергия и энтропия, в них принято состояние воды в тройной точке:

В этих таблицах термодинамические величины со штрихом относятся к кипящей воде с температурой насыщения (т.е. к параметрам на линии насыщения О – К , рис. 5.3), а величины с двумя штрихами – к сухому насыщенному пару (т.е. к параметрам на линии насыщения К – С ).

В таблицах насыщения по одному параметру (температуре или давлению) определяются величины .

В таблицах недогретой воды и перегретого пара параметры этих состояний разделены жирной горизонтальной чертой, выше которой – параметры воды, под чертой – параметры перегретого пара. Зная значения любых двух термодинамических параметра, можно определить значения остальных. Так, например, по заданным значениям давления р и температуры t находятся значения .

Кроме того, по физическим свойствам перегретый пар близок к идеальным газам и, следовательно, его термические параметры подчиняются уравнению Клайперона. Калорические параметры перегретого газа находятся аналогично, как для идеального газа – через изобарную и изохорную теплоемкости.

Экстенсивные параметры состояния влажного пара (объем V , внутренняя энергия U , энтальпия H и энтропия S ) определяются аддитивно из соответствующих величин для обеих фаз. Например, объем влажного пара равен сумме объемов кипящей воды и сухого насыщенного пара

,

а удельный объем влажного пара

.

Аналогично вычисляются и остальные параметры влажного пара со степенью сухости x

Количество теплоты, которое требуется для нагрева воды или водяного пара от температуры t 1 до температуры t 2 при постоянном давлении, определяется по формуле

.

5.4. hs -диаграмма водяного пара

На рис. 5.5 изображена hs -диаграмма водяного пара.

За начало координат в hs -диаграмме принято состояние в тройной точке. По оси абсцисс откладывается удельная энтропия s , а по оси ординат – удельная энтальпия h .

На диаграмму наносятся пограничные кривые воды и пара, соответственно, х = 0 и х = 1 (жирная кривая), изобары – p = const, изотермы – T = const и линии постоянной сухости – x = const. В области влажного пара (0 x v = const), которые на рис. 5.5 не изображены.

В практических расчетах обычно используется часть диаграммы для области влажного пара с большой степенью сухости (область диаграммы в верхнем правом углу), что дает возможность изобразить диаграмму в более крупном масштабе.

В практике могут встретиться паровые процессы, которые протекают полностью в области либо влажного, либо перегретого пара, либо так, что одна часть процесса протекает в области влажного, а другая – в области перегретого пара.

Исследование процесса состоит в определении начальных и конечных параметров пара, изменений внутренней энергии, энтальпии и подведенного (отведенного) количества теплоты.

Диаграмма позволяет по двум известным (независимым) термодинамическим параметрам определить все остальные.

По известным начальному и конечному состояниям процесса можно определить изменение внутренней энергии по формуле

.

Удельная теплота процесса определяется по формулам:

для изохорного процесса ( v =const)

;

для изобарного процесса ( p = const) ;

для изотермического процесса ( T = const) ;

для адиабатного (обратимого изоэнтропического) процесса ( s = const) .

Удельная работа процесса рассчитывается по формуле

.

Графический метод расчета по hs -диаграмме является наглядным, относительно малотрудоемким, но недостаточно точным. Для получения более точных данных используются соответствующие формулы и таблицы воды и водяного пара [10,11].

Перечислите все возможные состояния воды и водяного пара.

Как определяются термодинамические параметры для этих состояний воды и водяного пара?

Какие состояния водяного пара изображаются точками на пограничной кривой водяного пара?

При каких условиях происходит процесс парообразования?

Определение удельного объема, удельной энтальпии и удельной энтропии влажного пара.

Сколько параметров должно быть задано, чтобы определить все остальные для конкретного состояния воды или водяного пара?

Как изображаются основные термодинамические процессы в различных диаграммах водяного пара?

Как подсчитать внутреннюю энергию водяного пара?

Как рассчитать теплоту и работу в основных термодинамических процессах водяного пара?

6 . Влажный воздух

В атмосферном воздухе всегда есть влага в виде водяного пара, содержание которого зависит от метеоусловий, а также от наличия источников испарения воды и колеблется в широких пределах: от малых долей до 4 % (по массе). Влажность воздуха – важнейший параметр, определяющий комфортность окружающей среды, которая в помещениях искусственно поддерживается с помощью систем отопления, вентиляции и кондиционирования.

С атмосферным воздухом также приходится иметь дело в некоторых теплотехнических процессах (например, в процессе сушки). Воздух используется в качестве охладителя на тепловых электростанциях с циркуляционным оборотом воды, расположенных далеко от источников водоснабжения.

6.1. Основные понятия

Смесь сухого воздуха (не содержащего молекул воды) с водяным паром называется влажным воздухом .

Влажный воздух представляет собой один из частных случаев газовых смесей. Принципиальное отличие влажного воздуха от обычных газовых смесей заключается в том, что количество водяного пара в смеси не может быть произвольным: оно зависит от температуры и полного давления смеси и не может превышать определенного значения.

Для практики представляет интерес влажный воздух при атмосферном давлении B с температурами не ниже -50 ⁰С. При таких параметрах сухой воздух находится всегда в газообразном состоянии, тогда как водяной пар в зависимости от температуры смеси может перейти в жидкую или твердую фазу и вследствие этого выпадать из смеси.

В процессах изменения состояния влажного воздуха водяной пар может вводиться или удаляться из влажного воздуха, стабильным остается только масса сухого воздуха. Поэтому все характеризующие влажный воздух удельные величины относятся к 1 кг сухого воздуха, а не к 1кг смеси.

При невысоких давлениях (близких к атмосферному) и сухой воздух, и содержащийся в нем водяной пар можно рассматривать как идеальные газы.

Рассматривая влажный воздух как газовую смесь, по закону Дальтона (см. (1.4)) имеем:

р = р воздух + р пар или В = р воздух + р пар . (6.1)

Чем больше водяного пара находится в паровоздушной смеси, тем больше парциальное давление р пар . Влажный воздух, содержащий максимальное количество водяного пара при данной температуре (пар в насыщенном состоянии), называется насыщенным . В противном случае, воздух называется ненасыщенным (а пар в нем – перегретый).

Парциальное давление водяного пара при заданной температуре смеси (температуре влажного воздуха) не может превышать давления насыщения p s , т.е. р пар ≤ p s . Для ненасыщенного влажного воздуха – р пар p s , а для насыщенного – р пар = p s . Водяной пар, содержащийся в ненасыщенном влажном воздухе ( р пар p s ), находится в перегретом состоянии (см. рис. 5.1 и 5.2), его температура t > t s ( р пар ). Таким образом, ненасыщенный влажный воздух состоит из сухого воздуха и перегретого водяного пара, а насыщенный влажный воздух – из сухого воздуха и насыщенного водяного пара.

Водяной пар содержится в воздухе обычно в небольших количествах и в перегретом состоянии. Масса пара, содержащегося в 1 м 3 влажного воздуха, называется абсолютной влажностью :

,

т.е. абсолютная влажность численно равна плотности пара ρ пар при парциальном давлении р пар . Параметр D при заданной температуре может принимать значения от 0 (сухой воздух) до плотности насыщенного пара, равной 1/ v ” (насыщенный воздух).

Относительной влажностью воздуха называется отношение его реальной абсолютной влажности D к максимально возможной абсолютной влажности D max при той же температуре:

. (6.2)

Таким образом, относительная влажность определяется отношением парциального давления водяного пара к давлению насыщения при данной температуре (т.е. максимально возможному парциальному давлению водяного пара при этой температуре). Другими словами, относительная влажность отражает степень насыщения влажного воздуха водяным паром при данной температуре.

Во всех случаях φ ≤ 1. Обычно относительную влажность выражают в процентах. Для сухого воздуха φ = 0 , для насыщенного воздуха φ = 100 %.

Отношение массы пара к массе сухого воздуха называется влагосодержанием (или паросодержанием ):

.

Параметр d представляет собой массу влаги, приходящейся на 1 кг сухого воздуха. Эту безразмерную величину задают либо в кг/кг, либо в г/кг. Параметр d может принимать значения от 0 до ∞ .

Величину влагосодержания можно определить следующим образом. Уравнения состояния для сухого воздуха и водяного пара ( р воздух V = R воздух TM воздух и р пар V = R пар TM пар ) разделим почленно:

.

Найдем отсюда влагосодержание, подставив в это уравнение значение р воздух из закона Дальтона (6.1):

. (6.3)

Из уравнения видно, что с увеличением парциального давления пара влагосодержание увеличивается.

Максимальное значение влагосодержания зависит от температуры и давления влажного воздуха: при заданной температуре влажного воздуха максимум давления водяного пара равен давлению насыщения р s при этой температуре, следовательно, максимальное влагосодержание

.

Так как р s увеличивается с ростом температуры, то с ростом температуры влажного воздуха увеличивается и его максимальное влагосодержание.

Отсюда, в частности, следует: если влажный воздух находится при атмосферном давлении В , то при температуре влажного воздуха в 100 о С максимальное паросодержание d s = ∞ (чистый водяной пар).

Из уравнений (6.2) и (6.3) можно получить выражение, связывающее влагосодержание с относительной влажностью:

или .

Понижая температуру ненасыщенного влажного воздуха (φ Т = Т s ( р пар ) . Температура, при которой воздух с данным влагосодержанием d становится насыщенным (φ = 1), называется температурой точки росы и обозначается t p . При дальнейшем охлаждении влажного воздуха из него начнет выделяться вода в виде тумана или росы (происходит конденсация пара) и, следовательно, влагосодержание влажного воздуха d будет уменьшаться, при этом воздух будет оставаться влажным насыщенным (φ = 1).

6.2. Расчет параметров влажного воздуха

Газовая постоянная смеси двух идеальных газов – сухого воздуха и водяного пара – определяется выражением (см.(1.6)):

,

где r воздух и r пар – объемные доли соответственно сухого воздуха и водяного пара в смеси.

Из уравнения состояния идеального газа объемные доли можно вычислить как (см. (1.5))

.

Так как μ воздух = 28,96 кг/кмоль и μ пар = 18,016 кг/кмоль, то получаем

Запишем уравнение состояния влажного воздуха:

Отсюда плотность влажного воздуха определяется как

.

Из этого соотношения следует, что чем больше влажность воздуха (т.е. чем выше парциальное давление водяного пара в воздухе), тем меньше плотность воздуха. Следовательно, влажный воздух всегда легче, чем сухой.

Энтальпия влажного воздуха равна сумме энтальпий сухого воздуха и водяного пара. Отсюда удельная энтальпия влажного воздуха, отнесенная к единице массы сухого воздуха, определяется как:

.

Если за начало отсчета энтальпий сухого воздуха и водяного пара принять энтальпии при 0 о С, то удельная энтальпия сухого воздуха (кДж/кг) численно равна , где теплоемкость сухого воздуха при постоянном давлении (для малого интервала температур) равна

1 кДж/(кг·К), а удельная энтальпия сухого пара может быть определена по приближенной формуле , кДж/кг, где r – теплота парообразования, — удельная массовая изобарная теплоемкость.

Тогда удельная энтальпия влажного воздуха

, кДж/кг, (6.4)

где d берется с размерностью кг/кг.

6.3. hd -диаграмма влажного воздуха

Параметры влажного воздуха для практических целей определяют либо по таблицам, либо по диаграммам. Второй способ менее точный, но более наглядный.

Определение параметров влажного воздуха графическим способом рассмотрим с помощью hd -диаграммы, предложенной в 1918 г. проф. Л.К. Рамзиным.

На этой диаграмме все удельные величины относятся к 1 кг сухого воздуха. По оси ординат откладывается удельная энтальпия h (кДж/кг) влажного воздуха, а по оси абсцисс – влагосодержание d (г/кг) влажного воздуха. Для более удобного расположения различных линий (изотерм и линий постоянной относительной влажности) на диаграмме эти координатные оси составляют угол 135º (рис. 6.1). Таким образом, линии постоянного влагосодержания будут вертикальными прямыми, а линии постоянства энтальпии – наклонными прямыми.

Кроме того, на диаграмме нанесены (на рис. 6.1 они отсутствуют) следующие линии:

линии постоянных температур ненасыщенного влажного воздуха ( t = const). Так как энтальпия при фиксированной температуре t линейно зависит от влагосодержания d (6.4), то эти линии — прямые;

линии относительной влажности воздуха (φ = const);

линия парциального давления водяного пара.

Все поле диаграммы разделено на две части линией φ = 100%: выше её находится область ненасыщенного влажного воздуха, ниже линии – область перенасыщенного состояния воздуха.

Обычно диаграмма приводится для барометрического давления 0,09930 МПа (745 мм рт. ст.), но с достаточной степенью точности она может быть использована и для других близких давлений.

С помощью hd -диаграммы можно определить все необходимые параметры влажного воздуха: удельную энтальпию h , влагосодержание d , температуру t , температуру точки росы (на рис. 6.1 точка росы – точка С), относительную влажность φ, парциальное давление, если известны только два из этих параметров.

hd -диаграмма удобна не только для определения параметров состояния воздуха, но и для отображения изменений его состояния при нагревании, охлаждении, увлажнении, осушении и других процессов:

процесс нагревания влажного воздуха совершается при неизменном влагосодержании, т.е. при d = const (на диаграмме – вертикальная прямая О – А вверх от исходного положения);

процесс охлаждения влажного воздуха также протекает при d = const (вертикальная прямая вниз – О – В ). Этот процесс справедлив только до состояния полного насыщения воздуха, т.е. до φ = 100% (вертикальная прямая до пересечения с линией φ = 100% – О – С ). При дальнейшем охлаждении воздух окажется пересыщенным влагой, и она будет выпадать в виде росы на материале;

процесс конденсации можно считать проходящим по линии φ = 100% (продвижение от точки пересечения влево до пересечения с линией заданной конечной температурой – С – D ). Количество воды, образовавшейся в результате конденсации от точки С до точки D , на 1 кг сухого воздуха равно разности влагосодержаний d C – d D ;

адиабатный процесс увлажнения (осушения) в условиях постоянного давления происходит при неизменной энтальпии влажного воздуха ( h = const) и изобразится на hd -диаграмме отрезком О – Е . Здесь имеется в виду идеальный процесс насыщения влажного воздуха, т.е. не учитываются расход энергии на подогрев жидкости и связанные с этим потери в окружающую среду.

hd -диаграмма влажного воздуха широко используется в отопительно-вентиляционной практике и в теплотехнических расчетах, связанных с сушильной техникой.

Для сушки изделий используется воздух при t 1 = 25 о C с относительной влажностью φ = 50%. В воздушном подогревателе воздух нагревают до t 2 = 90 о C и направляют в сушилку, откуда он выходит при температуре t 3 = 35 о C. Определить конечное влагосодержание воздуха, расход количества теплоты и воздуха на 1 кг испаренной влаги. Процесс насыщения влажного воздуха считать идеальным.

в hd -диаграмме на пересечении изотермы t 1 = 25 о C и линии постоянной относительной влажности φ = 50 % находим точку, координаты которой определяют начальные влагосодержание и энтальпию ( d 1 = 10,0 г/кг и h 1 = 50,0 кДж/кг);

так как нагревание воздуха совершается при неизменном влагосодержании, то находим точку пересечения вертикальной прямой (процесс нагревания воздуха) с изотермой t 2 = 90 о C, которая характеризует состояние нагретого воздуха по выходе из подогревателя ( d 2 = 10,0 г/кг и h 2 = 117,5 кДж/кг);

из точки 2 проводим линию при i = const (так как теплота извне не поступает и процесс является адиабатным и изобарным одновременно) до пересечения с изотермой t 3 =35 о C. Эта точка пересечения характеризует состояние воздуха при выходе из сушилки ( d 3 = 32,0 г/кг и h 3 = 117,5 кДж/кг);

в рассматриваемом процессе сушки изделий из них испарилось, а в воздух добавилось, влаги M влаги = d 3 – d 1 = 32,0 –10,0 = 22,0 г/кг = 0,022 кг/кг (в расчете на 1 кг сухого воздуха);

поэтому для испарения 1 кг влаги потребуется М воздух = 1 кг : M влаги = 1 : 0,022 = 45,5 кг сухого нагретого воздуха;

расход количества теплоты на нагрев 1 кг воздуха в воздушном подогревателе составляет q = h 3 – h 1 = 117,5 – 50,0 = 67,5 кДж/кг;

расход количества теплоты на 1 кг испаренной влаги составит Q = q M воздух = 67,5·45,5 = 3070 кДж.

Дать понятие влажного воздуха. Перечислить основные термодинамические параметры, определяющие состояние влажного воздуха.

Почему вертикальная шкала для измерения энтальпии влажного воздуха в диаграмме Рамзина совпадает со шкалой для температуры?

Дать понятие точки росы.

В чем состоит практическое значение hd -диаграммы?

Источник статьи: http://gigabaza.ru/doc/134232-p5.html