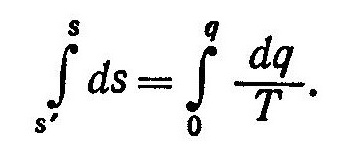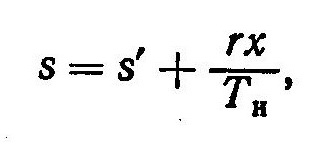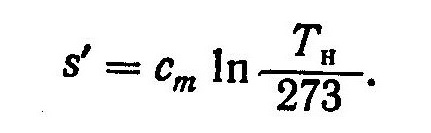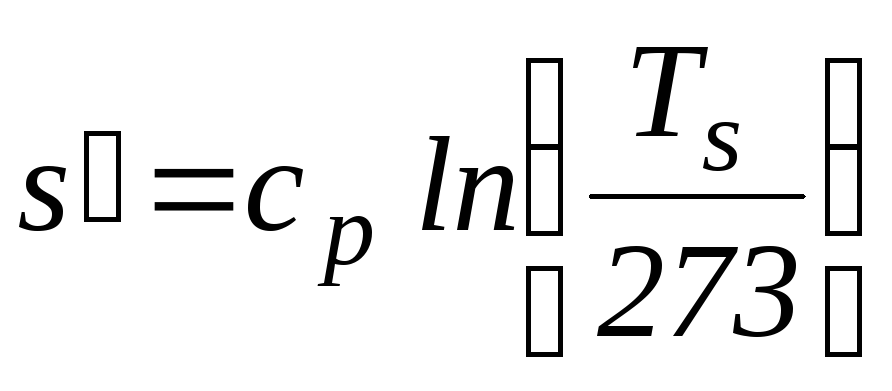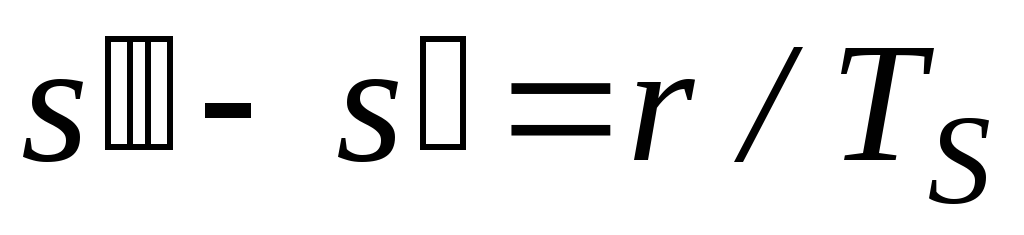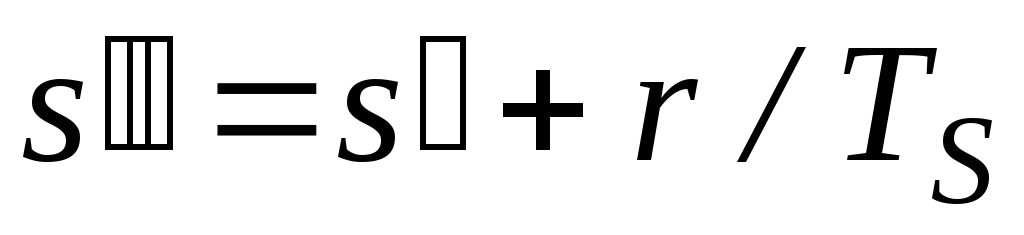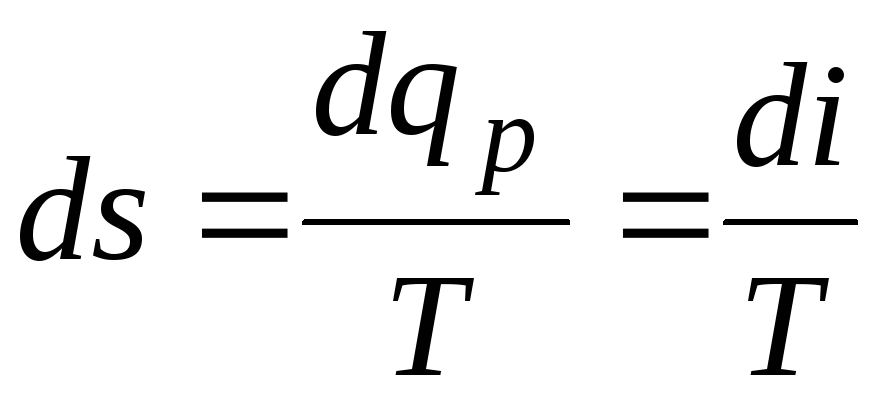Удельные объемы жидкости и пара.
Удельный объем жидкости зависит от температуры и давления. Однако последняя зависимость настолько незначительна, что практически ею пренебрегают.
Зависимость же удельного объема воды от температуры более заметна. Так, например, если при 0 о С и любом давлении удельный объем жидкой кипящей воды v’0 = 0,001 м 3 /кг, то при температуре 100 о С (и давлении
1 ата) v’ = 0,001043 м 3 /кг, а при температуре 200 о С (и давлении
16 ата) v’ = 0,001156 м 3 /кг.
Из этих данных следует, что при невысоких давлениях (точнее температурах) и этой зависимостью также можно пренебрегать, полагая, следовательно, что v’ = v’0 = 0,001 м 3 /кг.
Удельный объем сухого пара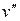 
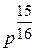
может быть найден для давлений до 10 ата по следующей формуле, полученной на основании опытов:
v” 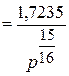= 1,7235, (5.1)
v” 
. (5.2)
Здесь р берется в ата.
Из этой формулы видно, что чем больше давление сухого пара, тем удельный объем его меньше, вследствие чего и отрезки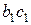 
, 
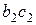
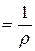
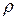
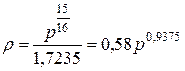
и т.д. (рис. 5.1) с повышением давления уменьшаются. Так как v” 
, где 
– плотность сухого пара, то, подставляя это значение v”в уравнение (5.1), получим, что
. (5.3)
Приближенно можно полагать, что при р около 10–15 ата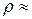 
0,5 р,
т.е., что плотность сухого пара численно равен половине давления.
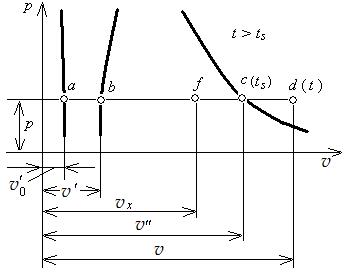
Рис. 5.6. Изображение удельных объемов воды в осях vр
при различных ее состояниях
Удельный объем влажного пара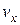 
находится в пределах между v’ и v” (рис. 5.6). Величина его зависит от степени сухости пара х. Если в 1 кг влажного пара содержится х кг сухого пара и (1 – х) кг воды, то эти х кг сухого пара будут занимать объем х v” м 3 /кг, а (1 – х) кг воды (1 – х) v’ v’м 3 /кг.
Так как влажный пар, применяемый в теплотехнике, имеет обычно большую степень сухости (порядка 0,9 и больше), то объемом воды, содержащейся в нем, можно пренебрегать, считая, что
Неточность, допускаемая при этом, получается незначительной.
При небольшой степени сухости пара и высоком давлении пользоваться упрощенным уравнением (5.5) нельзя, так как ошибка при этом может оказаться уже значительной. Практически это уравнение применяют к парам, имеющим степень сухости х не меньше 0,7.
Преобразуем уравнение (5.4), решив его относительно х:
.
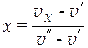
Обращаясь теперь к рис. 5.6, видим, что vх – v’ = bf, а v”– v’= bc.
х = 
.
Для нахождения удельного объема перегретого пара было предложено в разное время несколько уравнений, дающих приближенные результаты. Наиболее точным из них является уравнение проф. М.П. Вукаловича и проф. И.И. Новикова, однако оно очень сложно. Поэтому удельные объемы перегретого пара обычно находят по специальным таблицам, о которых говорится в разделе VI.
Дата добавления: 2015-09-07 ; просмотров: 2254 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник статьи: http://helpiks.org/5-9465.html
Параметры и функции состояния водяного пара
Здравствуйте! Водяной пар может быть трех видов: влажным насыщенным, сухим насыщенным, перегретым. Рассмотрим все три вида.
Влажный насыщенный пар. Удельный объем влажного насыщенного пара находится из выражения
где υ» — удельный объем сухого насыщенного пара; υ’ — удельный объем воды при температуре парообразования и том же давлении, что и объем υ».
Двумя штрихами в технической термодинамике принято обозначать параметры и функции состояния сухого насыщенного пара, а одним штрихом — величины, характеризующие состояние воды при температуре парообразования.
При небольших давлениях (p 0,8 объем жидкости υ'(1—х) можно не учитывать и приближенно определять удельный объем влажного насыщенного пара из соотношения υ ≈ υ»x. В процессе парообразования при постоянном давлении для получения 1 кг влажного насыщенного пара к 1 кг кипящей жидкости необходимо подвести количество теплоты
Так как в процессе при р = const количество теплоты равно изменению энтальпии, то величину энтальпии i влажного насыщенного пара можно определить из выражения
q = rx = i—i’ или i=i’+rx. (2)
Энтальпия i’ кипящей воды при температуре парообразования и теплота парообразования г соответствуют тому же давлению, что и энтальпия i. Так как величина энтальпии при 273 К принимается за нуль, то энтальпию i’ кипящей воды можно найти из выражения
где сm — средняя массовая теплоемкость воды в интервале температур от 273 К до Тн.
Энтальпия i’ кипящей воды, как следует из выражения (3), численно равна количеству теплоты, которая затрачивается для нагревания 1 кг воды от 0° С до температуры кипения tн при р = const.
В соответствии с уравнением первого закона термодинамики q = ∆u+l имеем
Анализ этого выражения показывает, что теплота парообразования r складывается из внутренней теплоты парообразования u»- u’, затрачиваемой на изменение внутренней энергии (преодоление сил притяжения между молекулами), и внешней теплоты парообразования p (u»- u’), равной работе против внешних сил. Для давлений меньше 20 МПа внешняя теплота парообразования незначительна и не превышает 13% от величины r.
Энтропию влажного насыщенного пара найдем из выражения
Так как в процессе парообразования при p=const T=const, то с учетом уравнения (1) получим
где s’— энтропия воды при температуре парообразования и том же давлении, что и величины s, г и Tн.
Величину s’ можно определить из соотношения
Пределы интегрирования в выражении (4) приняты в соответствии с условием, что при 273 К энтропия равна нулю.
Сухой насыщенный пар.
Состояние сухого насыщенного пара определяется значением одного параметра, например давления или температуры парообразования, так как другой параметр состояния — степень сухости — имеет определенное значение х=1. Параметры и функции состояния сухого насыщенного пара можно определить по выведенным выше формулам (1), (2) для влажного пара при условия х = 1.
Перегретый пар.
Для получения перегретого пара в котельном агрегате устанавливают специальный теплообменник (пароперегреватель), в котором происходит перегрев влажного насыщенного пара. Для характеристики состояния перегретого пара должны быть известны два любых параметра состояния пара, например давление и температура. Вместо параметров могут быть заданы функции состояния (энтальпия или энтропия).
Энтальпия перегретого пара находится из выражения
где сpm—массовая средняя изобарная теплоемкость пара в интервале температур от Tн до Т.
Энтропия перегретого пара определяется следующим образом
В уравнения (5) и (6) необходимо подставлять значения величин i», s» и cpm при том же давлении, для которого определяются энтальпия i и энтропия s. Исп.литература: 1) Теплотехника и теплотехническое оборудование предприятий промышленности строительных материалов и изделий, Н.М. Никифорова, Москва, «Высшая школа», 1981. 2) Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,»Вышейшая школа», 1976.
Источник статьи: http://teplosniks.ru/texnicheskaya-termodinamika/parametry-i-funkcii-sostoyaniya-vodyanogo-para.html
Основные параметры влажного насыщенного пара
Влажный насыщенный пар – это двухфазная смесь, представляющая собой пар со взвешенными в нем капельками жидкости. Поэтому значения удельного объема влажного пара vx находятся между значениями v и v и зависят от давления и степени сухости пара х:
, или 
(7.28)
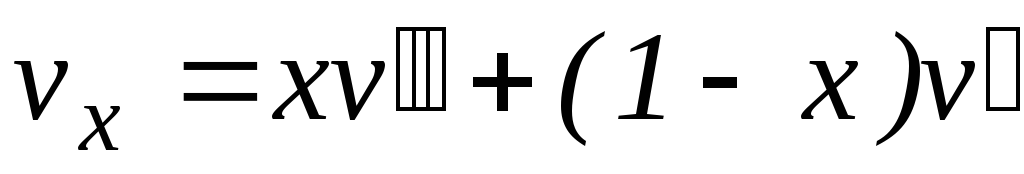
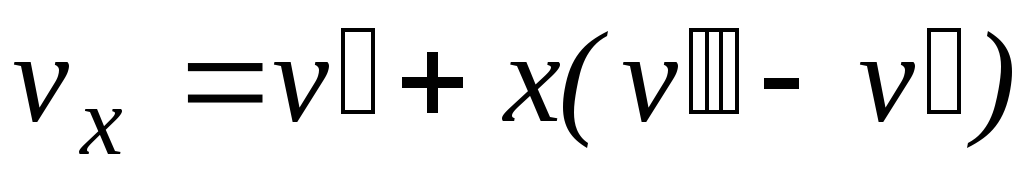
Состояние влажного насыщенного пара характеризуется двумя параметрами: давлением (или температурой насыщения при этом давлении) и степенью сухости х. Разность v — v выражает приращение объема пара в процессе парообразования. При малых давлениях удельный объем сухого насыщенного пара во много раз больше удельного объема воды. Например, при Р = 0,1 МПа удельный объем сухого насыщенного пара v в 1630 раз больше удельного объема воды при температуре кипения v, а при Р = 0,005 МПа – в 28000 раз. Поэтому при невысоких давлениях (ниже в 3 МПа) и больших степенях сухости (х 8), объемом воды (1-х)v можно пренебречь, и тогда:
, (7.29)
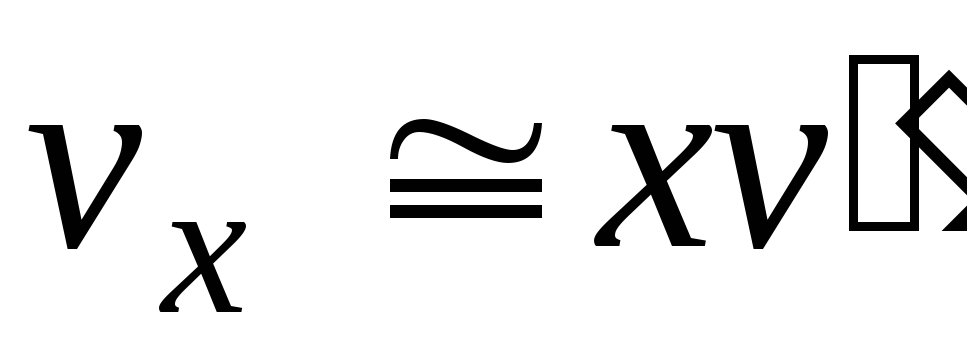
т.е. удельный объем влажного насыщенного пара приближенно равен произведению удельного объема сухого пара того же давления на степень сухости.
Плотность влажного пара определяется по формуле:
(7.30)
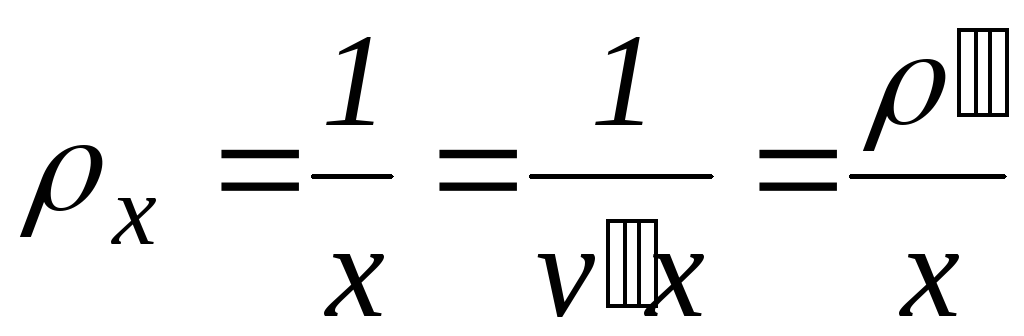
Таким образом, плотность влажного пара приближенно равна отношению плотности сухого пара к степени сухости.
Энтальпия влажного пара определяется по правилу аддитивности уравнением:
(7.31)
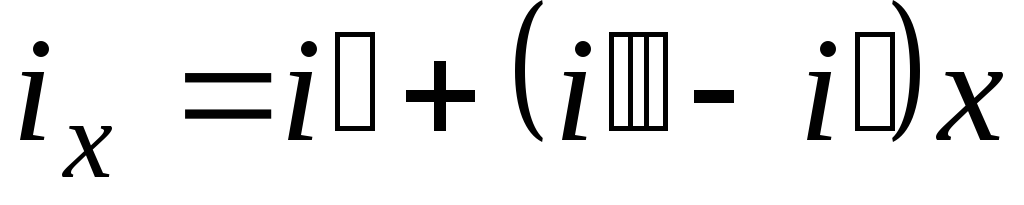
С учетом (7.18) имеем:
(7.32)
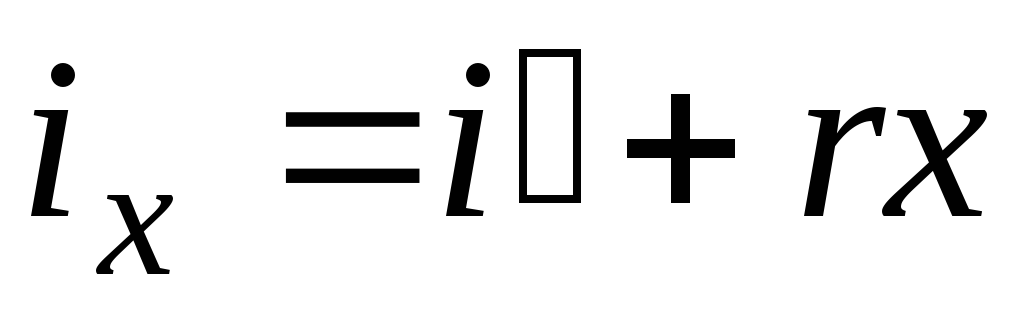
Внутренняя энергия влажного пара определяется по уравнению:
(7.33)
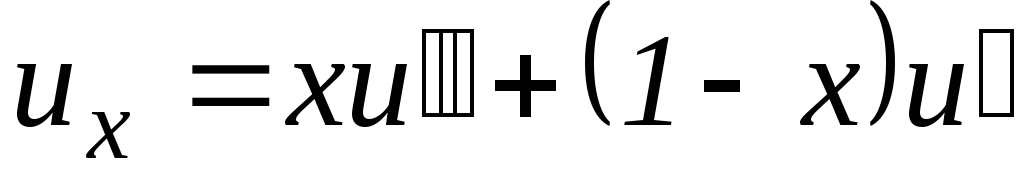
С учетом соотношения (7.30) уравнение (7.33) преобразуется к виду:
(7.34)
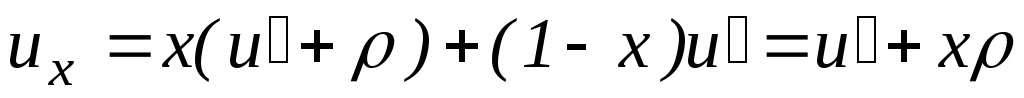
С другой стороны, для влажного пара, как и для любого состояния вещества, справедлива зависимость:
,
(7.35)
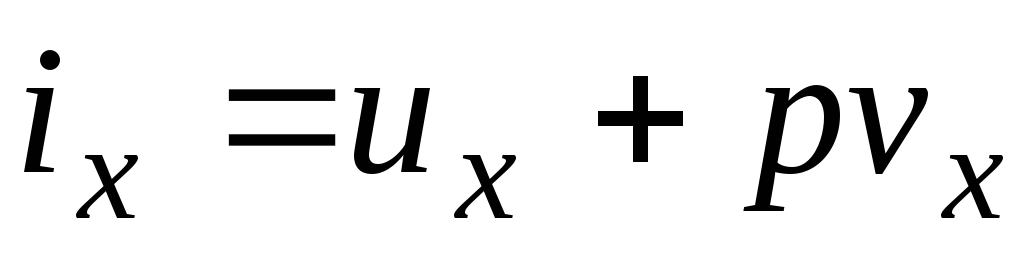
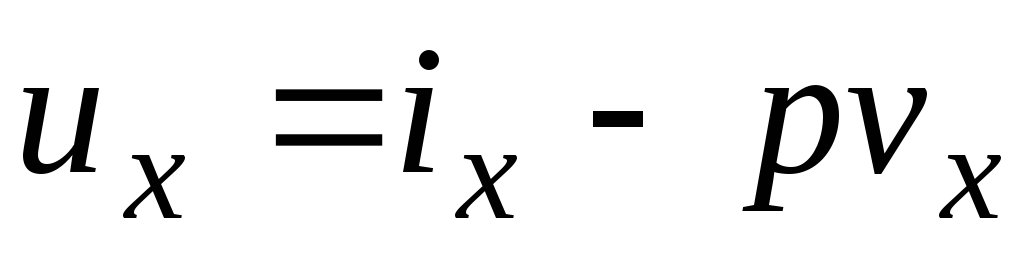
Энтропию влажного пара можно определить по правилу аддитивности:
(7.36)
(7.37)
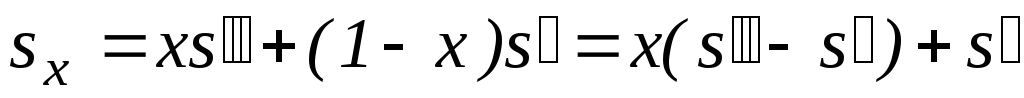
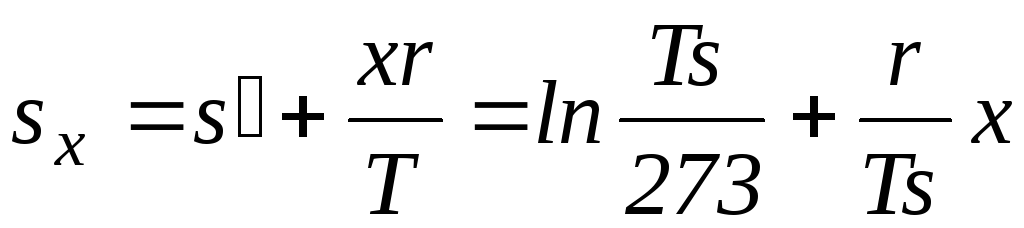
В выражении (7.37) первое слагаемое характеризует приращение энтропии при нагревании 1 кг воды до температуры кипения, второе – приращение энтропии при испарении х кг жидкости.
Степень сухости определяется по формуле:
(7.38)
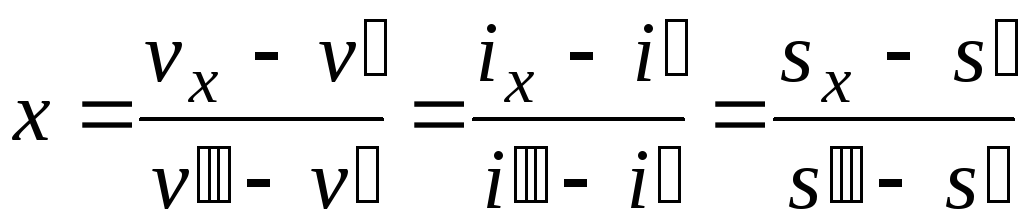
Теплота парообразования влажного пара определяется следующими соотношениями:
(7.39)
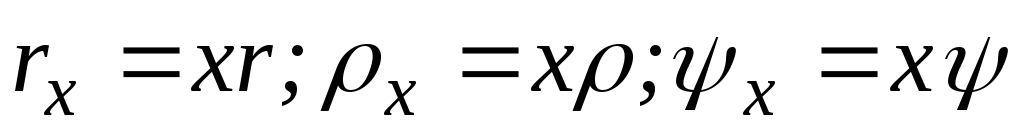
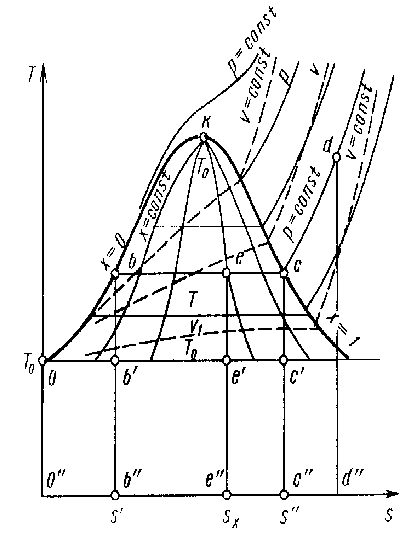
Диаграмма sTдля водяного пара
При вычислении удельной энтропии водяного пара ее условно принимают равной нулю (
= 0) в тройной точке для жидкой фазы (Т = 273,16 К для воды). Следовательно, в системе координат sT (рис. 7.3) тройная точка находится на оси температур при значении Т0 = 273,16 К (0,01С).
Приращение удельной энтропии жидкости при повышении ее температуры вдоль пограничной кривой от температуры ТА = 273,16 К до температуры Ts определяется по формуле:
следовательно, в координатах sT нижняя пограничная кривая изображается логарифмической кривой, берущей свое начало из точки с координатами s0 = 0; Т = 273,16 К.
При приближении к критическим параметрам удельная теплоемкость начинает с ростом температуры возрастать и при критической температуре стремится к бесконечности. В связи с этим нижняя пограничная кривая начинает отклоняться от логарифмической кривой (делается более пологой) и, наконец, вблизи критической точки меняет вогнутость.
Изобара жидкости по характеру (и по месту расположения) очень близка к нижней пограничной кривой.
Площадь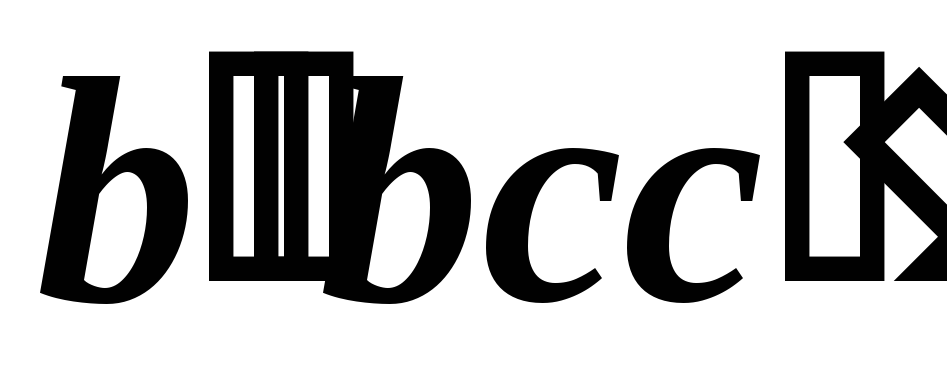 
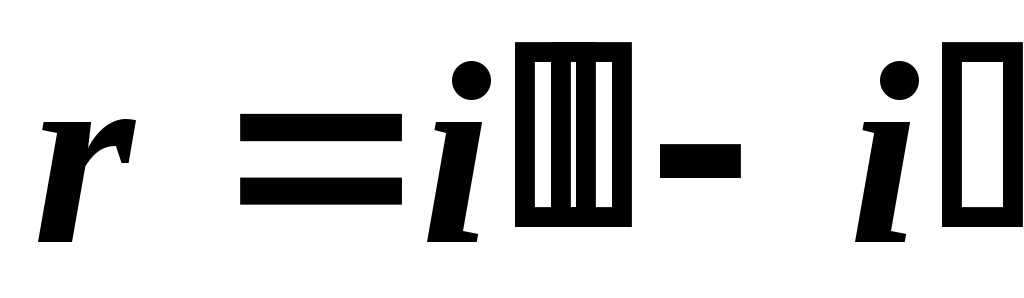
численно равна теплоте парообразования
.
В изобарном, одновременно являющимся изотермическим процессе парообразования приращение удельной энтропии находят по формуле:
и удельную энтропию сухого насыщенного пара – по формуле:
Откладывая от нижней пограничной кривой горизонтальные отрезки, равные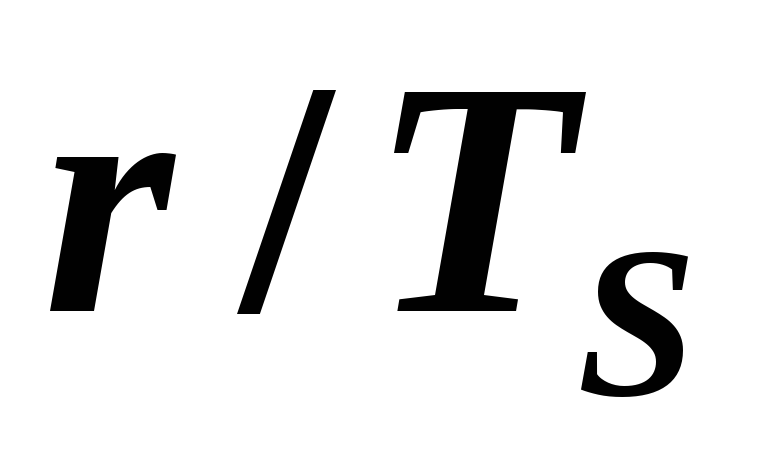 
, получаем ряд точек, принадлежащих верхней пограничной кривой. Следовательно, очертание верхней пограничной кривой зависит, , от удельной теплоты парообразованияr, от температуры насыщения Ts и от формы нижней пограничной кривой.
Изменение удельной энтропии в равновесном изобарном процессе перегрева пара:
,
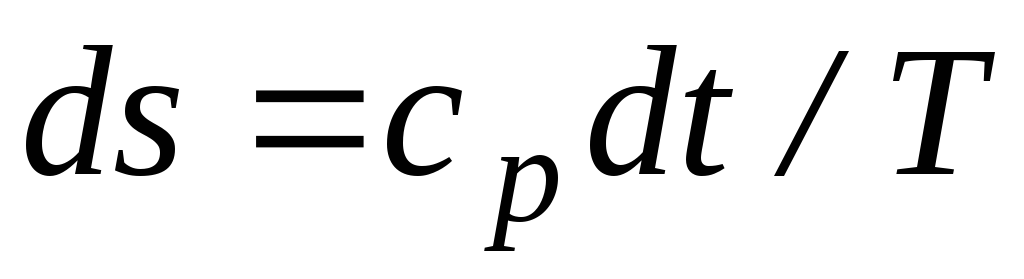
следовательно, изобара перегрева пара изображается логарифмической кривой.
Площадь 
численно равна теплоте перегрева
.
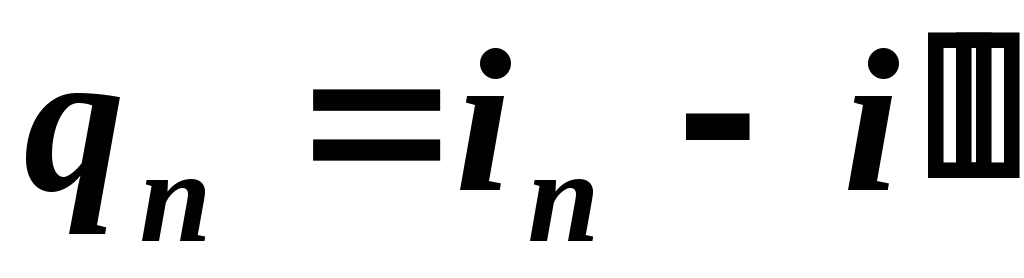
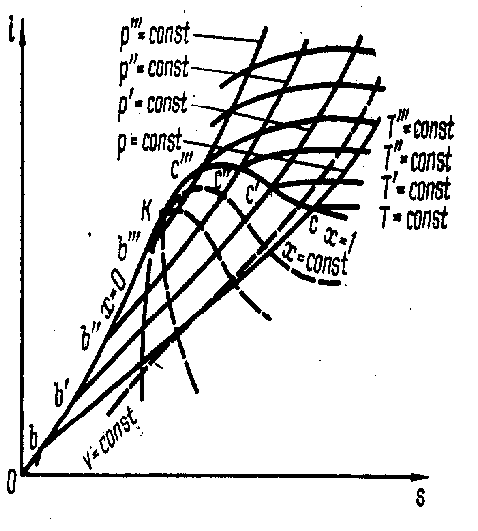
si-диаграмма водяного пара
Для изучения и расчетов различных термодинамических процессов удобно пользоваться si-диаграммой (рис. 7.4).
В системе координат si наносят пограничные кривые, изобары и изотермы (иногда и изохоры). За начало координат принимают состояние воды в тройной точке, где s0 = 0, i0 = 0. Состояние воды изображается точками на соответствующих изобарах, которые практически сливаются с пограничной кривой жидкости. Линии изобар в области влажного пара являются прямыми наклонными линиями, расходящимися веером от пограничной кривой сухого пара.
Угловой коэффициент наклона изобары к оси абсцисс численно равен абсолютной температуре данного состояния, т.к. в области влажного пара изобара совпадает с изотермой, то, согласно последнему уравнению, изобары влажного пара являются прямыми линиями:
а это и есть уравнение прямой линии.
В области перегретого пара изобары имеют кривизну с выпуклостью вниз.
В области влажного пара наносится сетка линий постоянной сухости пара (x = const), которые сходятся в критической точке К.
Изотермы в области влажного пара совпадают с изобарами. В области перегретого пара они расходятся: изобары поднимаются вверх, а изотермы представляют собой кривые линии, обращенные выпуклостью вверх. При низких давлениях изотермы близки к горизонтальным прямым. С повышением давления кривизна изотермы увеличивается.
На диаграмму наносится сетка изохор, которые имеют вид кривых, поднимающихся более круто вверх по сравнению с изобарами.
Обратимый адиабатный процесс в is-диаграмме изображается вертикальными прямыми.
Источник статьи: http://studfile.net/preview/5125939/page:23/
