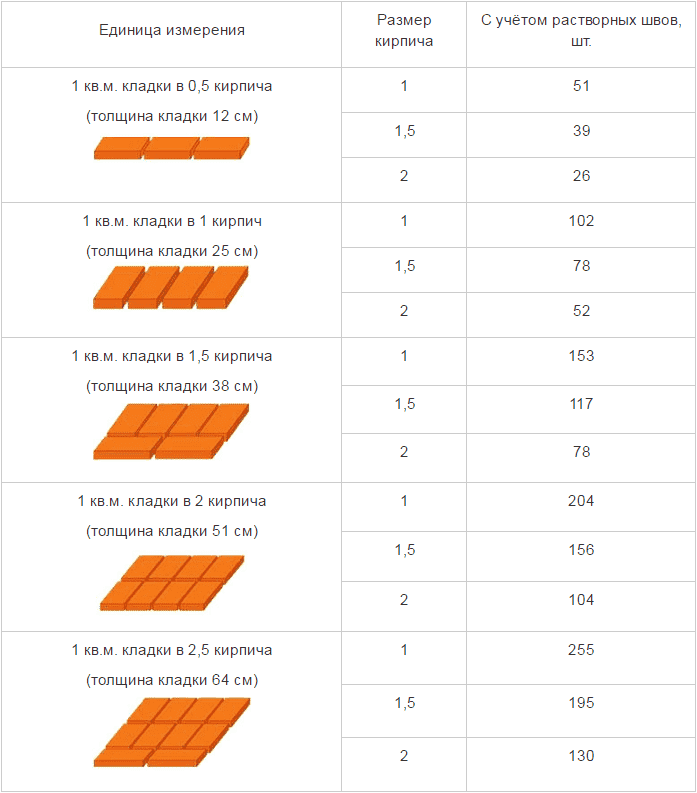
- Значения коэффициента В1 для насыщенного пара
- Показатели адиабаты: определение и процесс
- Адиабатический процесс
- Уравнение Пуассона для адиабаты идеального газа
- Что такое показатель адиабаты?
- Теплоемкости CP и CV
- Величина γ для газа идеального одноатомного
- Зависимость γ от числа степеней свободы
- Показатель адиабаты для смеси газов
- Показатель адиабаты
- Содержание
- Соотношения для идеального газа
- Соотношения с использованием количества степеней свободы
- Соотношения для реальных газов
- Термодинамические выражения
- Адиабатический процесс
- Экспериментальное определение величины показателя адиабаты
- См. также
- Примечания
- Смотреть что такое «Показатель адиабаты» в других словарях:
Значения коэффициента В1 для насыщенного пара
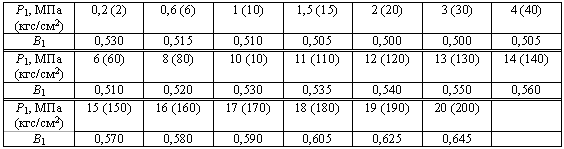
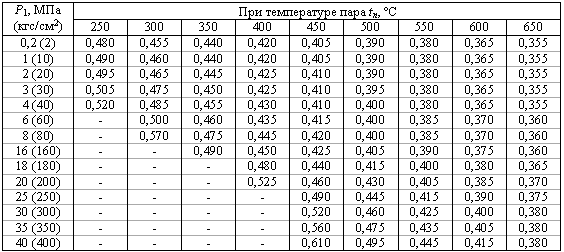
Значения коэффициента В1 для перегретого пара
или определяют по формуле:
для давления в МПа
для давления в кгс/см 2
где К — показатель адиабаты, равный 1,35 для насыщенного пара, 1,31 для перегретого пара;
Р1 — максимальное избыточное давление перед предохранительным клапаном, МПа;
V1 — удельный объем пара перед предохранительным клапаном, м 3 /кг.
(Измененная редакция, Изм. № 2).
Формула для определения пропускной способности клапана должна применяться только при условии: (Р2+0,1)≤(Р1+0,1) βкр для давления в МПа или (Р2+1)≤(Р1+1)βкр для давления в кгс/см 2 , где
Р2 — максимальное избыточное давление за предохранительным клапаном в пространстве, в которое истекает пар из котла (при истечении в атмосферу Р2 = 0 МПа (кгс/см 2 );
βкр — критическое отношение давлений.
Для насыщенного пара βкр=0,577, для перегретого пара βкр=0,546.
5.3. Коэффициент α принимают равным 90% от значения, полученного предприятием-изготовителем на основании проведенных испытаний.
МЕТОДЫ КОНТРОЛЯ
6.1. Все предохранительные клапаны должны быть испытаны на прочность, плотность, а также герметичность сальниковых соединений и уплотнительных поверхностей.
6.2. Объем испытаний клапанов, их порядок и методы контроля должны быть установлены в технических условиях на клапаны конкретного типоразмера.
СОДЕРЖАНИЕ
1. Общие требования
2. Требования к предохранительным клапанам прямого действия
3. Требования к предохранительным клапанам, управляемым при помощи вспомогательных устройств
4. Требования к подводящим и отводящим трубопроводам предохранительных клапанов
5. Пропускная способность предохранительных клапанов
6. Методы контроля
При устройстве газопровода, водопроводной и канализационной систем, а также других промышленных инженерных систем не обойтись без вентилей и задвижек. Многие считают, что вентили являются разновидностью задвижек, только меньшего размера, но на самом деле это разные устройства, имеющие существенные конструкционные отличия, определяющие особенности их эксплуатации. Вентили и задвижки имеют свои плюсы и минусы, которые и определяют оптимальный выбор устройства для конкретных условий применения.
Что такое вентиль и задвижка?
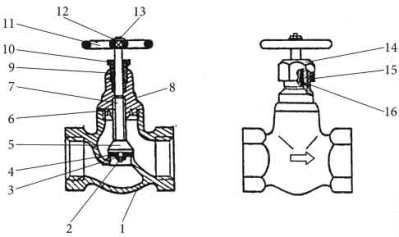
Вентиль – это прибор, который устанавливается на газо-, воздухо-, водо-, паро-, масло- и иные трубопроводы для открытия и закрытия проходных отверстий с помощью клапана. Вентиль состоит из стального, чугунного или бронзового корпуса, имеющего седло для клапана, самого клапана со шпинделем с винтовой нарезкой и рукоятки, обеспечивающей возможность вращения шпинделя. К трубопроводу вентили присоединяются с помощью резьбы или фланцев и подразделяются на муфтовые и фланцевые.
Вентиль в разрезе
Задвижка– это прибор, который устанавливается на трубопроводы для открытия и закрытия проходных отверстий с помощью клапана, перемещающегося перпендикулярно по отношению к оси потока рабочей среды. В зависимости от конструкции запорного органа задвижки подразделяются на шланговые, шиберные и параллельные. Шпинделя же могут быть выдвижными или вращаемыми.
Источник статьи: http://helpiks.org/5-91774.html
Показатели адиабаты: определение и процесс
При изучении поведения газов в физике много внимания уделяется изопроцессам, то есть таким переходам между состояниями системы, во время которых сохраняется один термодинамический параметр. Тем не менее, существует газовый переход между состояниями, который не является изопроцессом, но который играет важную роль в природе и технике. Речь идет об адиабатическом процессе. В данной статье рассмотрим его подробнее, акцентируя внимание на том, что такое показатель адиабаты газа.
Адиабатический процесс
Согласно термодинамическому определению, под адиабатическим процессом понимают такой переход между начальным и конечным состояниями системы, в результате которого не существует обмена теплом между внешней средой и изучаемой системой. Такой процесс возможен при наличии следующих двух условий:
- теплопроводность между внешней средой и системой по той или иной причине является низкой;
- скорость процесса велика, поэтому обмен теплом не успевает происходить.
В технике адиабатный переход используют как для разогрева газа при его резком сжатии, так и для его охлаждения во время быстрого расширения. В природе рассматриваемый термодинамический переход проявляет себя, когда воздушная масса поднимается или опускается по склону холма. Такие подъемы и спуски приводят к изменению точки росы в воздухе и к возникновению осадков.
Уравнение Пуассона для адиабаты идеального газа
Идеальный газ представляет собой систему, в которой частицы движутся хаотично с большими скоростями, не взаимодействуют друг с другом и являются безразмерными. Такая модель является очень простой с точки зрения ее математического описания.
Согласно определению адиабатного процесса, можно записать следующее выражение в соответствии с первым законом термодинамики:
Иными словами, газ, расширяясь или сжимаясь, совершает работу P*dV за счет соответствующего изменения своей внутренней энергии dU.
В случае идеального газа, если воспользоваться уравнением его состояния (закон Клапейрона-Менделеева), то можно получить следующее выражение:
Это равенство называется уравнением Пуассона. Люди, которые знакомы с физикой газов, заметят, что если величина γ будет равна 1, то уравнение Пуассона перейдет в закон Бойля-Мариотта (изотермический процесс). Однако такое преобразование уравнений невозможно, поскольку γ для любого типа идеального газа больше единицы. Величина γ (гамма) называется показателем адиабаты идеального газа. Рассмотрим подробнее его физический смысл.
Что такое показатель адиабаты?
Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом CP изобарную теплоемкость, а символом CV — изохорную. Тогда для γ справедливо равенство:
Поскольку γ всегда больше одного, то он показывает, во сколько раз изобарная теплоемкость изучаемой газовой системы превышает аналогичную изохорную характеристику.
Теплоемкости CP и CV
Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин CP и CV. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:
Величина CV определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.
Теперь предположим, что газ находится в сосуде с подвижным поршнем. В процессе нагрева такой системы поршень будет перемещаться, обеспечивая поддержание постоянного давления. Поскольку энтальпия системы в таком случае будет равна произведению изобарной теплоемкости на изменение температуры, то первый закон термодинамики примет вид:
Отсюда видно, что CP>CV, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.
Величина γ для газа идеального одноатомного
Самой простой газовой системой является одноатомный идеальный газ. Предположим, что мы имеет 1 моль такого газа. Напомним, что в процессе изобарного нагрева 1 моль газа всего на 1 Кельвин, он совершает работу, равную величине R. Этим символом принято обозначать универсальную газовую постоянную. Она равна 8,314 Дж/(моль*К). Применяя последнее выражение в предыдущем пункте для данного случая, получаем такое равенство:
Откуда можно определить значение изохорной теплоемкости CV:
Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:
Из последних двух равенств следует значение показателя адиабаты:
Отметим, что величина γ зависит исключительно от внутренних свойств самого газа (от многоатомности его молекул) и не зависит от количества вещества в системе.
Зависимость γ от числа степеней свободы
Выше было записано уравнение для изохорной теплоемкости одноатомного газа. Появившийся в нем коэффициент 3/2 связан с количеством степеней свободы у одного атома. У него существует возможность двигаться только в одном из трех направлений пространства, то есть существуют только поступательные степени свободы.
Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для CV приобретает вид:
Тогда значение γ будет равно:
Отметим, что на самом деле существует у двухатомной молекулы еще одна колебательная степень свободы, но при температурах в несколько сотен Кельвин она не задействуется и не вносит вклад в теплоемкость.
Если молекулы газа состоят из более, чем двух атомов, тогда у них будет 6 степеней свободы. Показатель адиабаты при этом будет равен:
Таким образом, при увеличении числа атомов в молекуле газа величина γ уменьшается. Если построить график адиабаты в осях P-V, то можно заметить, что кривая для одноатомного газа будет вести себя более резко, чем для многоатомного.
Показатель адиабаты для смеси газов
Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна ai. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:
Где γi — это величина γ для i-го компонента.
Например, это выражение можно применить для определения γ воздуха. Поскольку он состоит на 99 % из двухатомных молекул кислорода и азота, то его показатель адиабаты должен быть очень близок к значению 1,4, что подтверждается при экспериментальном определении этой величины.
Источник статьи: http://fb.ru/article/459900/pokazateli-adiabatyi-opredelenie-i-protsess
Показатель адиабаты
| Термодинамика |
|---|
 |
| Статья является частью одноименной серии. |
| Начала термодинамики |
| Уравнение состояния |
| Термодинамические величины |
| Термодинамические потенциалы |
| Термодинамические циклы |
| Фазовые переходы |
| править |
| См. также «Физический портал» |
Показатель адиабаты (иногда называемый коэффициентом Пуассона) — отношение теплоёмкости при постоянном давлении (
) к теплоёмкости при постоянном объёме (
). Иногда его ещё называют фактором изоэнтропийного расширения. Обозначается греческой буквой 
(гамма) или 
(каппа). Буквенный символ в основном используется в химических инженерных дисциплинах. В теплотехнике используется латинская буква 
[1] .
,
— теплоёмкость газа, 
— удельная теплоёмкость (отношение теплоёмкости к единице массы) газа, индексы 
и 
обозначают условие постоянства давления или постоянства объёма, соответственно.
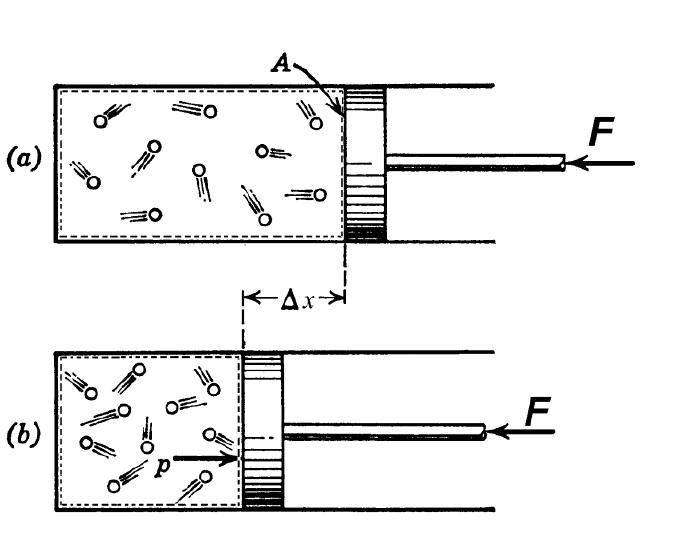
Для понимания этого соотношения можно рассмотреть следующий эксперимент:
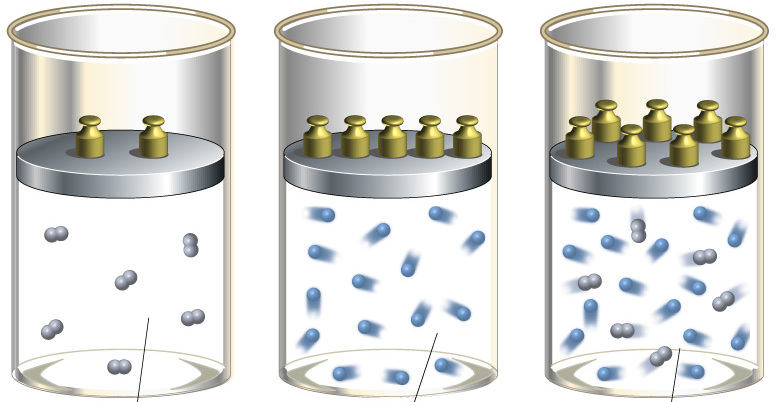
Закрытый цилиндр с закреплённым неподвижно поршнем содержит воздух. Давление внутри равно давлению снаружи. Этот цилиндр нагревается до определённой, требуемой температуры. Пока поршень не может двигаться, объём воздуха в цилиндре остаётся неизменным, в то время как температура и давление возрастают. Когда требуемая температура будет достигнута, нагревание прекращается. В этот момент поршень «освобождается» и, благодаря этому, начинает двигаться наружу без теплообмена с окружающей средой (воздух расширяется адиабатически). Совершая работу, воздух внутри цилиндра охлаждается ниже достигнутой ранее температуры. Чтобы вернуть воздух к состоянию, когда его температура опять достигнет упомянутого выше требуемого значения (при всё ещё «освобождённом» поршне) воздух необходимо нагреть. Для этого нагревания извне необходимо подвести примерно на 40 % (для двухатомного газа — воздуха) большее количество теплоты, чем было подведено при предыдущем нагревании (с закреплённым поршнем). В этом примере количество теплоты, подведённое к цилиндру с закреплённом поршне, пропорционально , тогда как общее количество подведённой теплоты пропорционально . Таким образом, показатель адиабаты в этом примере равен 1.4.
Другой путь для понимания разницы между и состоит в том, что применяется тогда, когда работа совершается над системой, которую принуждают к изменению своего объёма (то есть путём движения поршня, который сжимает содержимое цилиндра), или если работа совершается системой с изменением её температуры (то есть нагреванием газа в цилиндре, что вынуждает поршень двигаться). применяется только если 
— а это выражение обозначает совершённую газом работу — равно нулю. Рассмотрим разницу между подведением тепла при закреплённом поршне и подведением тепла при освобождённом поршне. Во втором случае давление газа в цилиндре остаётся постоянным, и газ будет как расширяться, совершая работу над атмосферой, так и увеличивать свою внутреннюю энергию (с увеличением температуры); теплота, которая подводится извне, лишь частично идёт на изменение внутренней энергии газа, в то время как остальное тепло идёт на совершение газом работы.
| Показатели адиабаты для различных газов [2] [3] | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Темп. | Газ | γ | Темп. | Газ | γ | Темп. | Газ | γ | ||
| −181 °C | H2 | 1.597 | 200 °C | Сухой воздух | 1.398 | 20 °C | NO | 1.400 | ||
| −76 °C | 1.453 | 400 °C | 1.393 | 20 °C | N2O | 1.310 | ||||
| 20 °C | 1.410 | 1000 °C | 1.365 | −181 °C | N2 | 1.470 | ||||
| 100 °C | 1.404 | 2000 °C | 1.088 | 15 °C | 1.404 | |||||
| 400 °C | 1.387 | 0°C | CO2 | 1.310 | 20 °C | Cl2 | 1.340 | |||
| 1000 °C | 1.358 | 20 °C | 1.300 | −115 °C | CH4 | 1.410 | ||||
| 2000 °C | 1.318 | 100 °C | 1.281 | −74 °C | 1.350 | |||||
| 20 °C | He | 1.660 | 400 °C | 1.235 | 20 °C | 1.320 | ||||
| 20 °C | H2O | 1.330 | 1000 °C | 1.195 | 15 °C | NH3 | 1.310 | |||
| 100 °C | 1.324 | 20 °C | CO | 1.400 | 19 °C | Ne | 1.640 | |||
| 200 °C | 1.310 | −181 °C | O2 | 1.450 | 19 °C | Xe | 1.660 | |||
| −180 °C | Ar | 1.760 | −76 °C | 1.415 | 19 °C | Kr | 1.680 | |||
| 20 °C | 1.670 | 20 °C | 1.400 | 15 °C | SO2 | 1.290 | ||||
| 0°C | Сухой воздух | 1.403 | 100 °C | 1.399 | 360 °C | Hg | 1.670 | |||
| 20 °C | 1.400 | 200 °C | 1.397 | 15 °C | C2H6 | 1.220 | ||||
| 100 °C | 1.401 | 400 °C | 1.394 | 16 °C | C3H8 | 1.130 | ||||
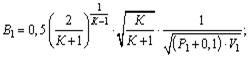
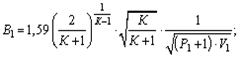
и внутренняя энергия может быть представлена как 
. Таким образом, можно также сказать, что показатель адиабаты — это отношение энтальпии к внутренней энергии:
):
— количество вещества в молях.
) молекул газа:
или 
,
.
.
), и эта разность отражает постоянство величины 
, то есть работы, совершаемой при расширении. Величина 
), во многих случаях являются недостаточно точными для практических инженерных расчётов, таких, как расчёты расходов через трубопроводы и клапаны. Предпочтительнее использовать экспериментальные значения, чем те, которые получены с помощью приближённых формул. Строгие значения соотношения 
может быть вычислено путём определения 
из свойств, выраженных как:
не составляет труда измерить, в то время как значения для 
— это давление и 
— объём газа.
— абсолютная температура в кельвинах; 
— молекулярная масса; 
— молярная масса.
.
. Для каждой ветви 2-х этапов можно написать соответствующие уравнения адиабаты и изохоры. Получится система уравнений, которые включают в себя показатель адиабаты. Их приближённое решение приводит к следующей расчетной формуле для искомой величины:
