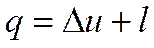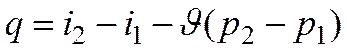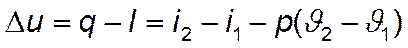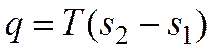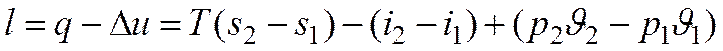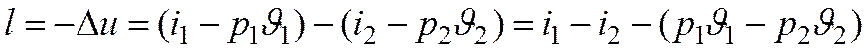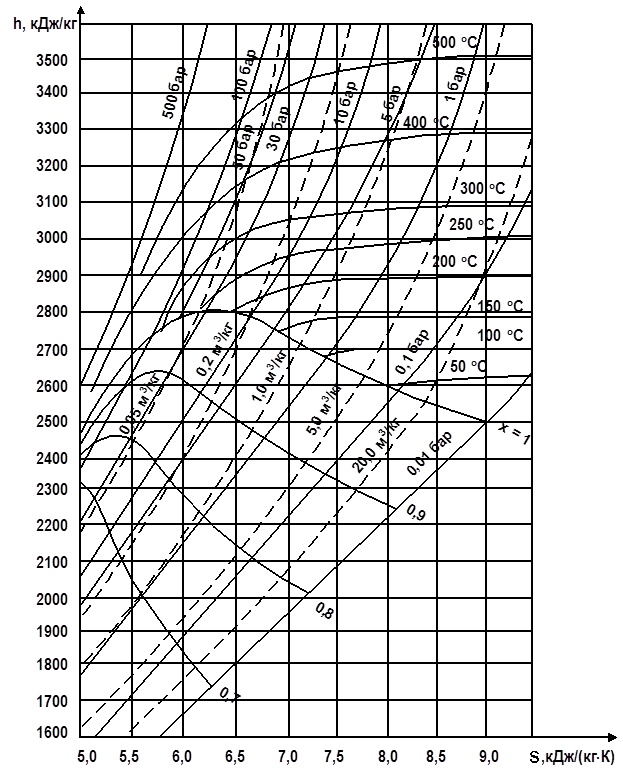Расчет процессов влажного пара

Расчет основных процессов водяного пара

Расчет процессов водяного пара состоит в определении параметров пара в начальном и конечном состояниях и вычислении подводимой теплоты, изменения внутренней энергии и работы изменения объема, связанных уравнением первого закона термодинамики

Для этого должны быть заданы значения двух каких-либо параметров в начальном состоянии пара и двух параметров в конечном состоянии.

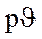
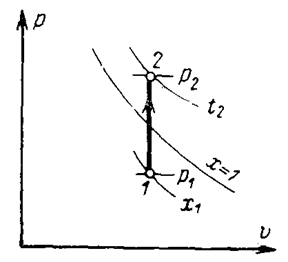
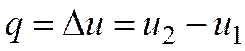
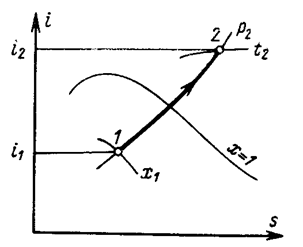
Изохорный процесс в –диаграмме изображается вертикальной прямой 1-2. В этом процессе l=0, поэтому для него

или

В is–диаграмме график этого процесса изображается линией 1-2. Начальная точка 1 находится на пересечении изобары р₁ и линии постоянной степени сухости х₁, а конечная точка 2 – на пересечении изобары р₂ и изотермы t₂.

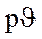
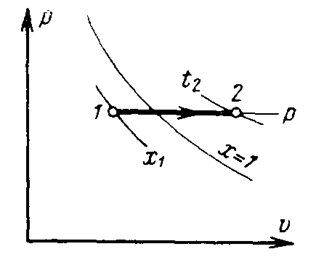
Изобарный процесс в –диаграмме изображается горизонтальной прямой. Для этого процесса

В is–диаграмме график этого процесса изображается линией 1-2, у которой начальная точка 1 находится на пересечении изобары процесса с линией степени сухости х₁, а конечная точка 2 – на пересечении той же изобары с изотермой t₂.

Изотермический процесс в 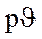–диаграмме изображается ломаной линией, которая в области влажного пара имеет вид горизонтальной прямой, а в области перегретого пара – кривой, постепенно переходящей в гиперболу.

Теплоту этого процесса можно представить формулой

В отличие от идеальных газов у водяного пара изотермический процесс сопровождается изменением внутренней энергии.

В соответствии с этим работа изменения объема:

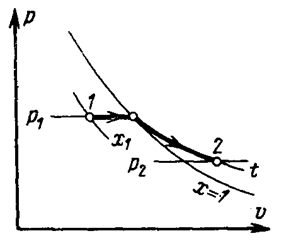
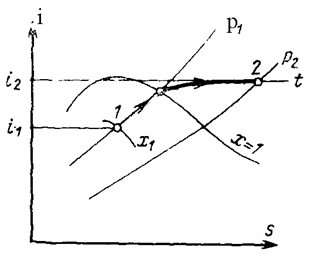
В is–диаграмме график этого процесса изображается ломаной линией 1-2, которая в области влажного пара имеет вид наклонной прямой, а в области перегретого пара – кривой, обращенной выпуклостью вверх и приближающейся к горизонтальной прямой. Начальная точка находится на пересечении изотермы процесса (совпадающей с изобарой р₁) с линией постоянной степени сухости х₁, а конечная точка – на пересечении той же изотермы с изобарой р₂.

Адиабатный процесс в 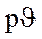–диаграмме изображается плавной кривой, более крутой, чем верхняя пограничная кривая.

В этом процессе q=0, поэтому

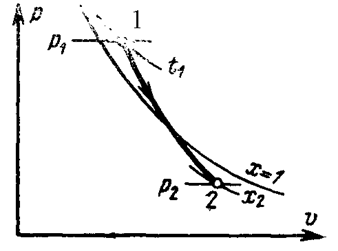
При адиабатном расширении перегретого пара он становится сначала сухим насыщенным, а затем влажным, причем с понижением давления степень сухости его уменьшается.

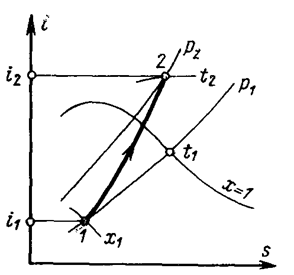
В is–диаграмме график этого процесса имеет вид вертикальной прямой 1-2. Начальная точка этого процесса 1 находится на пересечении изобары р₁ с изотермой t₁, а конечная точка 2 – на пересечении изобары р₂ с линией постоянной степени сухости х₂.

Источник статьи: http://helpiks.org/6-87646.html

Расчет процессов водяного пара

Расчет процессов водяного пара заключается в определении всех параметров начального и конечного состояния, теплоты и работы процесса.

Параметры начального и конечного состояний определяются с помощью диаграмм или по таблицам. Способ расчета с помощью таблиц более точен и не имеет ограничений. Способ с использованием h,s -диаграммы более прост, нагляден, но возможен только для влажного насыщенного пара с х > 0,6, сухого насыщенного пара и перегретого пара.

Изменение внутренней энергии для процесса определяется по уравнению:

Расчетные формулы для теплоты q, работы ℓ приведены в таблице 2.

Процесс	Работа изменения объема	Теплота
Изохорный	ℓ = 0	q = u2 – u1 = (h2 – h1) — v∙( p 2 – p1)
Изобарный	ℓ = q – Δu ℓ = p(v2 –v1)	q = h2 – h1
Изотермический	ℓ = q — Δu	q = T∙(s2 – s1)
Адиабатный	ℓ = (u2 – u1)	q = 0

Задача 3.3.Определить параметры влажного водяного пара при давлении 2,0 МПа и степени сухости 0,9.

Решение. Из таблиц водяного пара находим параметры кипящей воды «′» и сухого насыщенного пара «″» при 2,0 МПа:

р	tн	v′	v″	h′	h″	r	s′	s″
МПа	ºC	м 3 /кг	м 3 /кг	кДж/кг	кДж/кг	кДж/кг	кДж/ (кг·К)	кДж/ (кг·К)
2,0	212,37	0,00118	0,0995	908,6	2797,4	1888,8	2,4468	6,3373

По этим данным определятся параметры пара:

v = v˝·x + v΄·(1–x) = 0,0995·0,9 + 0,00118·0,1 = 0,098 м 3 /кг,

h = h΄+ r·x = 908,6 + 1888,8·0,9 = 2608,52 кДж/кг.

s = s΄+ (r·x)/T_S = 2,4468 + (1888,8·0,9)/485,52 = 5,95 кДж/(кг·К)

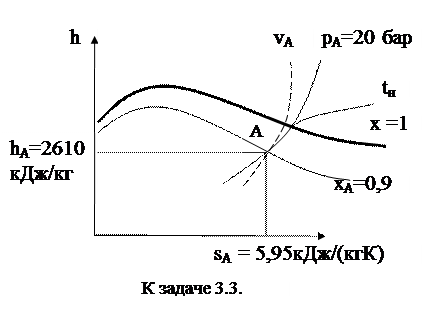Можно определить параметры пара по по h,s – диаграмме:

Задача 3.4. 1кг водяного пара, начальное состояние которого задано параметрами р₁=50 бар (5·10 3 кПа), t₁=400 ºC, расширяется адиабатно до давления р₂=0,5 бар (50 кПа).

Построить процесс в h,s; р,v; и Т,s – диаграммах.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник статьи: http://studopedia.su/10_119144_raschet-protsessov-vodyanogo-para.html

Расчет термодинамических процессов водяного пара

Таблицы термодинамических свойств воды и водяного пара

Для определения параметров состояния воды и водяного пара служат таблицы термодинамических (теплофизических) свойств воды и водяного пара. Современные таблицы составлены с использованием Международной системы единиц СИ. В таблицах приняты следующие обозначения физических величин и их размерности:

p – давление, Па: 1 МПа = 10 3 кПа = 10 6 Па = 10 бар;

Т – температура, К;

t – температура, о С:

v – удельный объем, м 3 /кг;

h – удельная энтальпия, кДж/кг;

s – удельная энтропия, кДж/(кг×град).

В термодинамических расчетах принято параметры (кроме p и t) обозначать для жидкости при температуре насыщения (кипения) индексом «штрих» (v‘, h‘, s‘), для сухого насыщенного пара индексом «два штриха» (v», h», s»), а для влажного насыщенного пара индексом «х» (v_х, h_х, s_х). В таблицах приводятся также значения удельной теплоты парообразования r = h» – h‘ и разности энтальпии в состоянии насыщения s» и s‘.

Для влажного насыщенного пара (степень сухости 0

Причем, v‘ t_н параметры воды и пара находятся по таблице перегретого пара

При p £ p_кр = 22,115 МПа таблица поделена горизонтальной линией на две части: верхняя – для области жидкости; нижняя – для перегретого пара. Граница раздела этих областей проходит при t = t_н.

При p > p_кр нет видимого фазового перехода воды в пар и вещество остается однородным (жидкость или пар). Условная граница между жидкостью и паром в этом случае может приниматься по критической изотерме.

Внутренняя энергия для воды и водяного пара в таблицах не приводится, она определяется по формуле:

Если u и h имеют размерность кДж/кг, то давление должно быть выражено в кПа, а удельный объем в м 3 /кг.

Диаграмма h – S(энтальпия – энтропия) находит широкое применение при расчетах паровых процессов и циклов теплоэнергетических установок.

Для практических целей диаграмма h – s выполняется не для всех фазовых областей воды, а только для ограниченной области водяного пара (рис. 2.17).

На рабочей диаграмме h – s наносится густая сетка изобар, изохор, изотерм и линий постоянной степени сухости х. Как уже отмечалось, в области влажного насыщенного пара изотерма совпадает с изобарой, причем геометрически это прямые линии. Чем выше давление, тем изобара круче и ближе к оси ординат.

На практике расчету подлежат четыре основных термодинамических процесса изменения состояния воды и водяного пара: изобарный (p = const), изохорный (v = const), изотермический (Т = const), адиабатный (dq = 0). Изображение указанных процессов в диаграммах p – v и T – s показано на рис. 2.15 и 2.16.

Состояние влажного насыщенного пара определяется в технике давлением р и степенью сухости х. Точка, изображающая этот состояние, находится на пересечении изобары и линии х = const. Состояние перегретого пара определяется давлением р и температурой t. Точка, изображающая состояние перегретого пара лежит на пересечении соответствующей изобары и изотермы.

Рис. 2.17 Рабочая h–s диаграмма водяного пара

Расчеты основных процессов водяного пара можно проводить как аналитическим, так и графическим методом, с применением h – s диаграммы. Аналитический метод сложен из-за громоздкости уравнений состояния водяного пара.

В таблице 2.4 приведены расчетные формулы для определения количества теплоты, работы изменения объема, и изменения внутренней энергии для основных термодинамических процессов.

Таблица 2.4: Расчетные формулы основных термодинамических процессов

Источник статьи: http://studopedia.ru/3_205749_raschet-termodinamicheskih-protsessov-vodyanogo-para.html

Водяной пар

Общие положения. Определение параметров состояния водяного пара. Pv — Тs — и hs – диаграммы состояния водяного пара. Процесс парообразования в паровых диаграммах.

Процесс парообразования. Основные понятия и определения. Рассмотрим про­цесс получения пара. Для этого 1 кг во­ды при температуре 0 °С поместим в ци­линдр с подвижным поршнем. Приложим к поршню извне некоторую постоянную силу Р. Тогда при площади поршня F давление будет постоянным и равным p=P/F. Изобразим процесс парообразо­вания, т. е. превращения вещества из жидкого состояния в газообразное, в р,v-диаграмме

Начальное состояние воды, находя­щейся под давлением р и имеющей тем­пературу 0°С, изобразится на диаграм­ме точкой a0. При подводе теплоты к воде ее температура постепенно повышается до тех пор, пока не достигнет температу­ры кипения ts, соответствующей данному давлению. При этом удельный объем жидкости сначала уменьшается, дости­гает минимального значения при t=4°С, а затем начинает возрастать. (Такой аномалией — увеличением плот­ности при нагревании в некотором диа­пазоне температур — обладают немногие жидкости. У большинства жидкостей удельный объем при нагревании увели­чивается монотонно). Состояние жидко­сти, доведенной до температуры кипения, изображается на диаграмме точкой а’.

При дальнейшем подводе теплоты начинается кипение воды с сильным увеличением объема. В цилиндре теперь на­ходится двухфазная среда — смесь воды и пара, называемая влажным насы­щенным паром. По мере подвода теплоты количество жидкой фазы умень­шается, а паровой — растет. Температу­ра смеси при этом остается неизменной и равной ts, так как вся теплота расходу­ется на испарение жидкой фазы. Следовательно — процесс парообразования на этой стадии является изобарно-изотермическим. Наконец, последняя капля во­ды превращается в пар, и цилиндр ока­зывается заполненным только паром, ко­торый называется сухим насыщенным. Состояние его изображается точ­кой а».

Рисунок 1 — р-v-диаграмма водяного пара

Насыщенным называется пар, находящийся в термическом и динамиче­ским равновесии с жидкостью, из кото­рой он образуется. Динамическое равно­весие заключается в том, что количество молекул, вылетающих из воды в паровое пространство, равно количеству молекул, конденсирующихся на ее поверхности. В паровом пространстве при этом равно­весном состоянии находится максималь­но возможное при данной температуре число молекул. При увеличении темпера­туры количество молекул, обладающих энергией, достаточной для вылета в па­ровое пространство, увеличивается. Рав­новесие восстанавливается за счет воз­растания давления пара, которое ведет к увеличению его плотности и, следова­тельно, количества молекул, в единицу времени конденсирующихся на поверхности воды. Отсюда следует, что давление насыщенного пара является монотонно возрастающей функцией его температу­ры, или, что то же самое, температура насыщенного пара есть монотонно воз­растающая функция его давления.

При увеличении объема над повер­хностью жидкости, имеющей температу­ру насыщения, некоторое количество жидкости переходит в пар, при уменьше­нии объема «излишний» пар снова пере­ходит в жидкость, но в обоих случаях давление пара остается постоянным.

Насыщенный пар, в котором отсут­ствуют взвешенные частицы жидкой фа­зы, называется сухим насыщенным паром. Его удельный объем и темпера­тура являются функциями давления. По­этому состояние сухого пара можно за­дать любым из параметров — давлением, удельным объемом или температурой.

Двухфазная смесь, представляющая собой пар со взвешенными в нем капель­ками жидкости, называется влажным насыщенным паром. Массовая до­ля сухого насыщенного пара во влажном называется степенью сухости па­ра и обозначается буквой х. Массовая доля кипящей воды во влажном паре, равная 1-х, называется степенью влажности. Для кипящей жидкости х=0, а для сухого насыщенного пара х=1. Состояние влажного пара характе­ризуется двумя параметрами: давлением (или температурой насыщения ts, опре­деляющей это давление) и степенью су­хости пара.

При сообщении сухому пару теплоты при том же давлении его температура будет увеличиваться, пар будет перегре­ваться. Точка а изображает состояние перегретого пара ив зависимости от температуры пара может лежать на разных расстояниях от точки а». Таким образом, перегретым называется пар, температура которого превышает температуру насыщенного пара того же давления.

Так как удельный объем перегретого пара при том же давлении больше, чем насыщенного, то в единице объема пере­гретого пара содержится меньшее коли­чество молекул, значит, он обладает меньшей плотностью. Состояние перегретого пара, как и любого газа, определя­ется двумя любыми независимыми пара­метрами.

Если рассмотреть процесс парообра­зования при более высоком давлении, то можно заметить следующие изменения. Точка a0, соответствующая состоянию 1 кг воды при 0 °С и новом давлении, остается почти на той же вертикали, так как вода практически несжимаема. Точ­ка а’ смещается вправо, ибо с ростом давления увеличивается температура ки­пения, а жидкость при повышении темпе­ратуры расширяется. Что же касается пара (точка а»), то, несмотря на увели­чение температуры кипения, удельный объем пара все-таки падает из-за более сильного влияния растущего давления.

Поскольку удельный объем жидкости растет, а пара падает, то при постоянном увеличении давления мы достигнем та­кой точки, в которой удельные объемы жидкости и пара сравняются. Эта точка называется критической. В критиче­ской точке различия между жидкостью и паром исчезают. Для воды параметры критической точки К составляют: ркр=221,29·105 Па; tкр = 374,15 °С; vкр = 0,00326 м3/кг.

Критическая температура — это мак­симально возможная температура сосу­ществования двух фаз: жидкости и на­сыщенного пара. При температурах, больших критической, возможно су­ществование только одной фазы. Назва­ние этой фазы (жидкость или перегретый пар) в какой-то степени условно и определяется обычно ее температурой. Все газы являются сильно перегретыми сверх Tкр парами. Чем выше температура перегрева (при данном давлении), тем ближе пар по своим свойствам к идеаль­ному газу.

Наименьшим давлением, при котором еще возможно равновесие воды и насы­щенного пара, является давление, соот­ветствующее тройной точке. Под последней понимается то единственное состояние, в котором могут одновремен­но находиться в равновесии пар, вода и лед (точка А’ на рисунке). Параметры тройной точки для воды: р0 = 611 Па; t0 = 0,01 °С; v0=0,00100 м3/кг. Процесс парообразования, происходящий при абсолютном давлении р0=611 Па, показан на диаграмме изобарой А’А», которая практически совпадает с осью абсцисс. При более низких давлениях пар может сосуществовать лишь в равновесии со льдом. Процесс образования пара непо­средственно из льда называется субли­мацией.

Если теперь соединить одноименные точки плавными кривыми, то получим нулевую изотерму I, каждая точка которой соответствует состоянию 1 кг во­ды при 0°С и давлении р, нижнюю пограничную кривую II, пред­ставляющую зависимость от давления удельного объема жидкости при темпе­ратуре кипения, и верхнюю погра­ничную кривую III, дающую зави­симость удельного объема сухого насы­щенного пара от давления.

Все точки горизонталей между кри­выми II и III соответствуют состояниям влажного насыщенного пара, точки кри­вой II определяют состояние кипящей воды, точки кривой III — состояния сухого насыщенного пара. Влево от кривой II до нулевой изотермы лежит область некипящей однофазной жидкости, впра­во от кривой III — область перегретого пара. Таким образом, кривые II и III определяют область насыщенного пара, отделяя ее от области воды и перегретого пара, и поэтому называются пограничными. Выше точки К, где погра­ничных кривых нет, находится область однофазных состояний, в которой нельзя провести четкой границы между жидкостью и паром.

Определение параметров воды и па­ра. Термодинамические параметры кипя­щей воды и сухого насыщенного пара берутся из таблиц теплофизических свойств воды и водяного пара. В этих таблицах термодинамические величины со штрихом относятся к воде, нагретой до температуры кипения, а величины с двумя штрихами — к сухому насыщен­ному пару.

Поскольку для изобарного процесса подведенная к жидкости теплота , то, при­менив это соотношение к процессу а’а», получим

.

Величина r называется теплотой парообразования и определяет количество теплоты, необходимое для превращения одного килограмма воды в сухой насыщенный пар той же темпе­ратуры.

Приращение энтропии в процессе па­рообразования определяется формулой

.

За нулевое состояние, от которого отсчитываются величины s‘, принято состояние воды в тройной точке. Так как состояние кипящей воды и сухого насы­щенного пара определяется только од­ним параметром, то по известному давле­нию или температуре из таблиц воды и водяного пара берутся значения v‘, v» , h‘, h» ,s‘, s«, r.

Удельный объем vx, энтропия sx и эн­тальпия hx влажного насыщенного пара определяются по правилу аддитивности. Поскольку в 1 кг влажного пара содер­жится x кг сухого и кг кипящей воды, то

.

;

;

Непосредственно из таблиц взять па­раметры влажного пара нельзя. Их опре­деляют по приведенным выше формулам по заданному давлению (или температу­ре) и степени сухости.

Однофазные состояния некипящей воды и перегретого пара задаются двумя параметрами. По заданным давлению и температуре из таблиц воды и перегре­того пара находят значения v, h, s.

Т — s-диаграмма водяного пара. Для исследования различных процессов с во­дяным паром кроме таблиц используется Т — s-диаграмма. Она строится путем переноса числовых данных таблиц водяного пара в Т — s-координаты.

Рисунок 2 — T — s-диаграмма водяного пара

Состояние воды в тройной точке (s0 = 0; T0 = 273,16 К) изображается в диаграмме точкой А’. Откладывая на диаграмме для разных температур значения s‘ и s«, получим нижнюю и верх­нюю пограничные кривые. Влево от ни­жней пограничной кривой располагается область жидкости, между пограничными кривыми — двухфазная область влажно­го насыщенного пара, вправо и вверх от верхней пограничной кривой — область перегретого пара.

На диаграмму наносят изобары, изохоры и линии постоянной степени су­хости, для чего каждую изобару а’а» делят на одинаковое число частей и сое­диняют соответствующие точки линиями x = const. Область диаграммы, лежащая ниже нулевой изотермы, отвечает раз­личным состояниям смеси пар+лед.

h— s-диаграмма водяного пара. Если за независимые параметры, определяю­щие состояние рабочего тела, принять энтропию s и энтальпию h, то каждое состояние можно изобразить точкой на h-s-диаграмме.

На рисунке 6.3 изображена h, s-диаграм­ма для водяного пара, которая строится путем переноса числовых данных таблиц водяного пара в h—s-координаты.

За начало координат принято состоя­ние воды в тройной точке. Откладывая на диаграмме для различных давлений значения s‘ и h» для воды при температу­ре, кипения, а также s« и h« для сухого насыщенного пара, получаем нижнюю и верхнюю пограничные кривые.

Рисунок 3 — h-s-диаграмма водяного пара

Изобары в двухфазной области влаж­ного пара представляют собой пучок рас­ходящихся прямых. Действительно, в процессе р=const , или , т. е. тангенс угла на­клона изобары в h, s-координатах числен­но равен абсолютной температуре данно­го состояния. Так как в области насыще­ния изобара совпадает с изотермой, тангенс угла наклона постоянен и изо­бара является прямой. Чем выше давле­ние насыщения, тем выше температура, тем больше тангенс угла наклона изо­бары, поэтому в области насыщения пря­мые р = const расходятся. Чем больше давление, тем выше лежит изобара. Кри­тическая точка К лежит не на верши­не, как это было в р — v— и Т — s-диаграммах, а на левом склоне пограничной кри­вой.

В области перегрева температура па­ра (при постоянном давлении) растет с увеличением s примерно по логарифми­ческой кривой и крутизна изобары увели­чивается. Аналогичный характер имеют изобары и в области воды, но они идут так близко от пограничной кривой, что практически сливаются с ней.

При низких давлениях и относитель­но высоких температурах перегретый пар по своим свойствам близок к идеальному газу. Так как в изотермическом процессе энтальпия идеального газа не изменяет­ся, изотермы сильно перегретого пара идут горизонтально. При приближение к области насыщения, т. е. к верхней пограничной кривой, свойства перегрето­го пара значительно отклоняются от свойств идеального газа и изотермы искривляются.

В h— s-диаграмме водяного пара нанесены также линии v=const, идущие круче изобар.

Обычно всю диаграмму не выполня­ют, а строят только ее верхнюю часть, наиболее употребительную в практике расчетов. Это дает возможность изобра­жать ее в более крупном масштабе.

Для любой точки на этой диаграмме можно найти р, v, t, h, s, x. Большое достоинство диаграммы состоит в том, что количество теплоты в изобарном про­цессе равно разности ординат конечной и начальной точек процесса и изобража­ется отрезком вертикальной прямой, а не площадью как в Т-s-диаграмме, поэтому h—s-диаграмма исключительно широко используется при проведении тепловых расчетов.

Основные термодинамические про­цессы водяного пара. Для анализа рабо­ты паросиловых установок существенное значение имеют изохорный, изобарный, изотермический и адиабатный процессы. Расчет этих процессов можно выполнить либо с помощью таблицы воды и водяно­го пара, либо с помощью h, s-диаграммы. Первый способ более точен, но второй более прост и нагляден.

Общий метод расчета по h—s-диаг­рамме состоит в следующем. По извест­ным параметрам наносится начальное состояние рабочего тела, затем прово­дится линия процесса и определяются его параметры в конечном состоянии. Далее вычисляется изменение внутрен­ней энергии, определяются количества теплоты и работы в заданном процессе.

Изохорный процесс. Из диаграммы на рисунке видно, что нагреванием при постоянном объеме влажный пар можно перевести в сухой насыщен­ный и перегретый. Охлаждением его можно сконденсировать, но не до конца, так как при каком угодно низком давле­нии над жидкостью всегда находится не­которое количество насыщенного пара. Это означает, что изохора не пересекает нижнюю пограничную кривую.

Рисунок 4 — Изохорный процесс водяного пара.

Изменение внутренней энергии водного пара при v=const

.

Данная формула справедлива и для всех без исключения остальных термоди­намических процессов.

В изохорном процессе работа 1=0, поэтому подведенная теплота расходует­ся (в соответствии с первым законом термодинамики) на увеличение внутрен­ней энергии пара:

Изобарный процесс. При подводе теплоты к влажному насыщен­ному пару его степень сухости увеличи­вается и он (при постоянной температу­ре) переходит в сухой, а при дальнейшем подводе теплоты — в перегретый пар (температура пара при этом растет). При отводе теплоты влажный пар конденсируется при Ts= const.

Полученная в процессе теплота рав­на разности энтальпий:

.

Работа процесса подсчитывается по формуле:

.

Рисунок 5 — Изобарный процесс водяного пара

Изотермический процесс. Внутренняя энергия водяного пара в процессе T = const не остается постоян­ной (как у идеального газа), так как изменяется ее потенциальная составляю­щая. Величина находится по формуле .

Количество полученной в изотерми­ческом процессе теплоты равно

.

Работа расширения определяется из первого закона термодинамики:

.

Рисунок 6 — Изотермический процесс водяного пара

Адиабатный процесс. При адиабатном расширении давление и температура пара уменьшаются, и перегре­тый пар становится сначала сухим, а за­тем влажным. Работа адиабатного про­цесса определяется выражением

.

Рисунок 7 — Адиабатный процесс водяного пара

Уравнение состояния реальных га­зов

В реальных газах в отличие от иде­альных существенны силы межмолеку­лярных взаимодействий (силы притяже­ния, когда молекулы находятся на значи­тельном расстоянии, и силы отталкивания при достаточном сближении их друг с другом) и нельзя пренебречь собствен­ным объемом молекул.

Наличие межмолекулярных сил от­талкивания приводит к тому, что молеку­лы могут сближаться между собой толь­ко до некоторого минимального расстоя­ния. Поэтому можно считать, что свобод­ный для движения молекул объем будет равен , где b — тот наименьший объем, до которого можно сжать газ. В соответствии с этим длина свободного пробега молекул уменьшается и число ударов о стенку в единицу времени, а следовательно, и давление увеличива­ется по сравнению с идеальным газом в отношении , т. е.

.

Силы притяжения действуют в том же направлении, что и внешнее давле­ние, и приводят к возникновению молеку­лярного (или внутреннего) давления. Сила молекулярного притяжения каких-либо двух малых частей газа пропорцио­нальна произведению числа молекул в каждой из этих частей, т. е. квадрату плотности, поэтому молекулярное давле­ние обратно пропорционально квадрату удельного объема газа: рмол = а/v2, где а — коэффициент пропорциональности, зависящий от природы газа.

Отсюда получаем уравнение Ван-дер-Ваальса (1873 г.):

,

или

.

При больших удельных объемах и сравнительно невысоких давлениях ре­ального газа уравнение Ван-дер-Ваальса практически вырождается в уравнение состояния идеального газа Клапейрона, ибо величина a/v2

(по сравнению с p) и b (по сравнению с v) становятся прене­брежимо малыми.

Уравнение Ван-дер-Ваальса с ка­чественной стороны достаточно хорошо описывает свойства реального газа, но результаты численных расчетов не всег­да согласуются с экспериментальными данными. В ряде случаев эти отклонения объясняются склонностью молекул ре­ального газа к ассоциации в отдельные группы, состоящие из двух, трех и более молекул. Ассоциация происходит вслед­ствие несимметричности внешнего элек­трического поля молекул. Образовавши­еся комплексы ведут себя как самостоя­тельные нестабильные частицы. При столкновениях они распадаются, затем вновь объединяются уже с другими мо­лекулами и т. д. По мере повышения тем­пературы концентрация комплексов с большим числом молекул быстро уменьшается, а доля одиночных молекул растет. Большую склонность к ассоциа­ции проявляют полярные молекулы во­дяного пара.

Источник статьи: http://pandia.ru/text/78/050/79836.php